Review of Clustering Methods for Functional Data

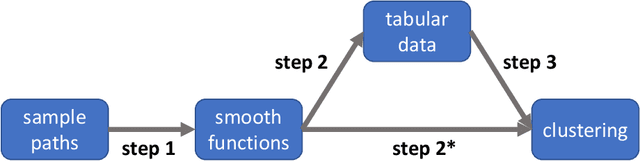
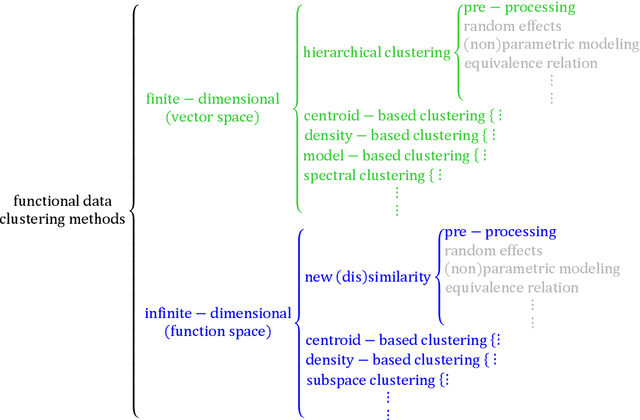
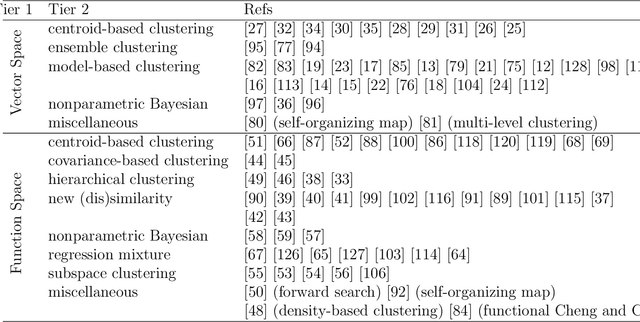
Functional data clustering is to identify heterogeneous morphological patterns in the continuous functions underlying the discrete measurements/observations. Application of functional data clustering has appeared in many publications across various fields of sciences, including but not limited to biology, (bio)chemistry, engineering, environmental science, medical science, psychology, social science, etc. The phenomenal growth of the application of functional data clustering indicates the urgent need for a systematic approach to develop efficient clustering methods and scalable algorithmic implementations. On the other hand, there is abundant literature on the cluster analysis of time series, trajectory data, spatio-temporal data, etc., which are all related to functional data. Therefore, an overarching structure of existing functional data clustering methods will enable the cross-pollination of ideas across various research fields. We here conduct a comprehensive review of original clustering methods for functional data. We propose a systematic taxonomy that explores the connections and differences among the existing functional data clustering methods and relates them to the conventional multivariate clustering methods. The structure of the taxonomy is built on three main attributes of a functional data clustering method and therefore is more reliable than existing categorizations. The review aims to bridge the gap between the functional data analysis community and the clustering community and to generate new principles for functional data clustering.

Bayesian Optimisation for Sequential Experimental Design with Applications in Additive Manufacturing

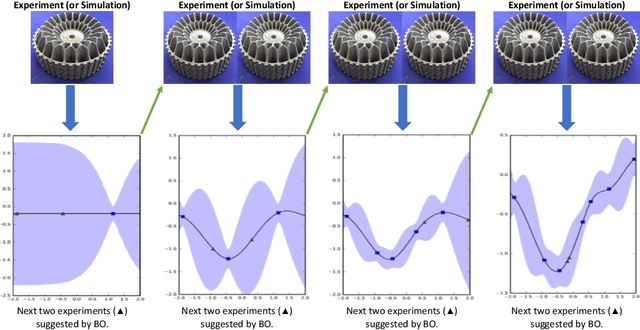
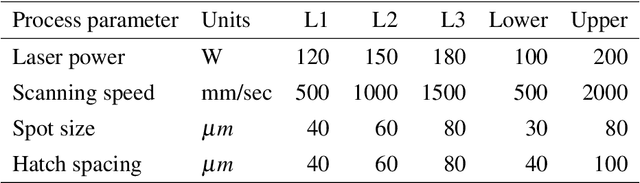
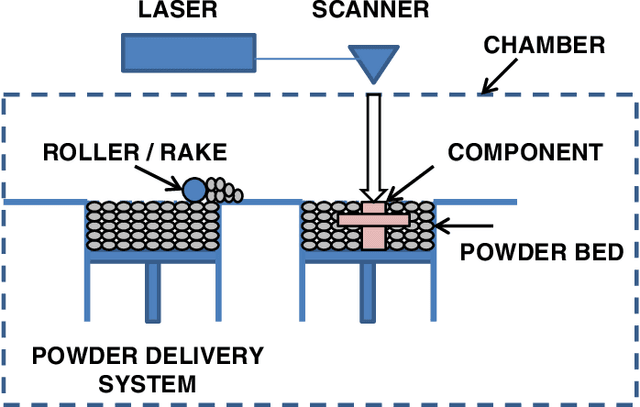
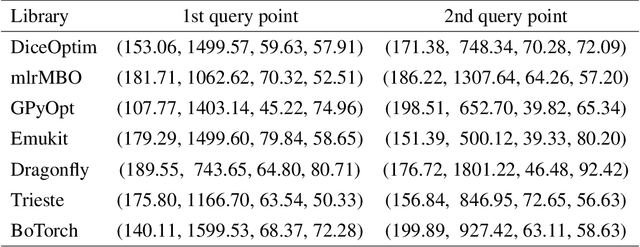
Bayesian optimization (BO) is an approach to globally optimizing black-box objective functions that are expensive to evaluate. BO-powered experimental design has found wide application in materials science, chemistry, experimental physics, drug development, etc. This work aims to bring attention to the benefits of applying BO in designing experiments and to provide a BO manual, covering both methodology and software, for the convenience of anyone who wants to apply or learn BO. In particular, we briefly explain the BO technique, review all the applications of BO in additive manufacturing, compare and exemplify the features of different open BO libraries, unlock new potential applications of BO to other types of data (e.g., preferential output). This article is aimed at readers with some understanding of Bayesian methods, but not necessarily with knowledge of additive manufacturing; the software performance overview and implementation instructions are instrumental for any experimental-design practitioner. Moreover, our review in the field of additive manufacturing highlights the current knowledge and technological trends of BO.

Clustering of Big Data with Mixed Features

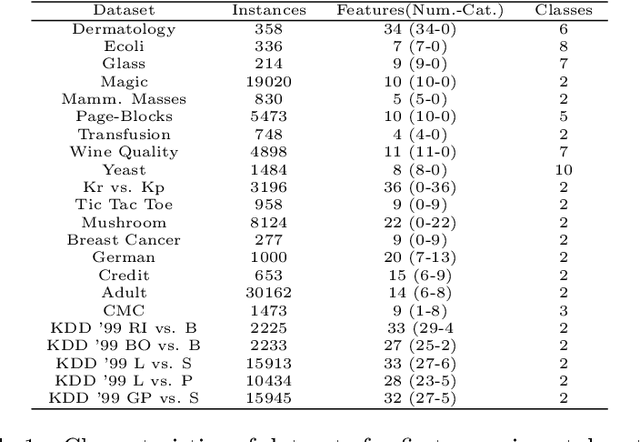
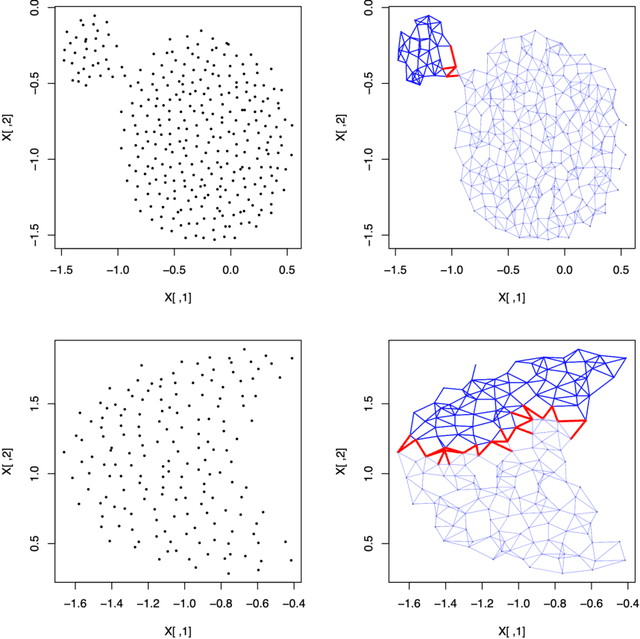
Clustering large, mixed data is a central problem in data mining. Many approaches adopt the idea of k-means, and hence are sensitive to initialisation, detect only spherical clusters, and require a priori the unknown number of clusters. We here develop a new clustering algorithm for large data of mixed type, aiming at improving the applicability and efficiency of the peak-finding technique. The improvements are threefold: (1) the new algorithm is applicable to mixed data; (2) the algorithm is capable of detecting outliers and clusters of relatively lower density values; (3) the algorithm is competent at deciding the correct number of clusters. The computational complexity of the algorithm is greatly reduced by applying a fast k-nearest neighbors method and by scaling down to component sets. We present experimental results to verify that our algorithm works well in practice. Keywords: Clustering; Big Data; Mixed Attribute; Density Peaks; Nearest-Neighbor Graph; Conductance.

Weighted Clustering Ensemble: A Review

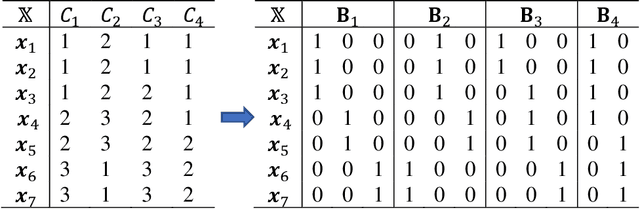
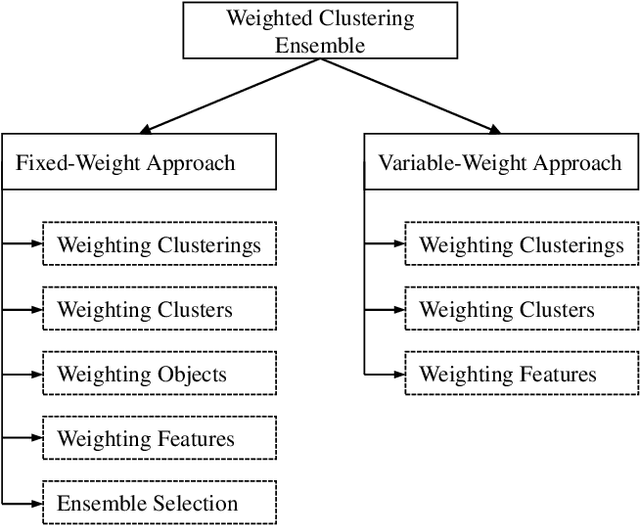
Clustering ensemble has emerged as a powerful tool for improving both the robustness and the stability of results from individual clustering methods. Weighted clustering ensemble arises naturally from clustering ensemble. One of the arguments for weighted clustering ensemble is that elements (clusterings or clusters) in a clustering ensemble are of different quality, or that objects or features are of varying significance. However, it is not possible to directly apply the weighting mechanisms from classification (supervised) domain to clustering (unsupervised) domain, also because clustering is inherently an ill-posed problem. This paper provides an overview of weighted clustering ensemble by discussing different types of weights, major approaches to determining weight values, and applications of weighted clustering ensemble to complex data. The unifying framework presented in this paper will help clustering practitioners select the most appropriate weighting mechanisms for their own problems.