Jose Carlos Ferreira da Rocha
Inference with Seperately Specified Sets of Probabilities in Credal Networks
Dec 12, 2012

Abstract:We present new algorithms for inference in credal networks --- directed acyclic graphs associated with sets of probabilities. Credal networks are here interpreted as encoding strong independence relations among variables. We first present a theory of credal networks based on separately specified sets of probabilities. We also show that inference with polytrees is NP-hard in this setting. We then introduce new techniques that reduce the computational effort demanded by inference, particularly in polytrees, by exploring separability of credal sets.
Inference in Polytrees with Sets of Probabilities
Oct 19, 2012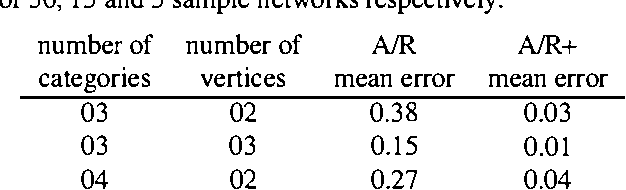
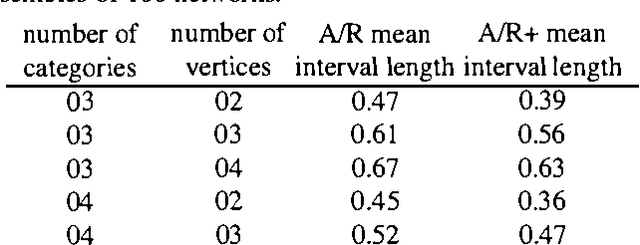
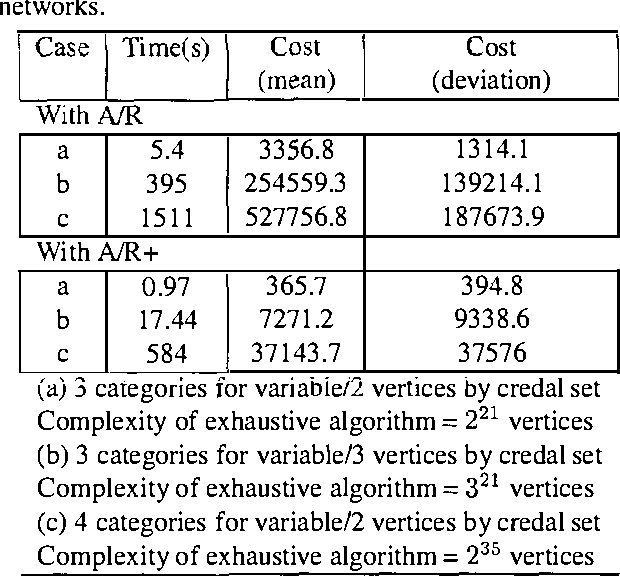
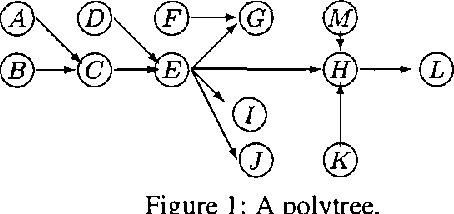
Abstract:Inferences in directed acyclic graphs associated with probability sets and probability intervals are NP-hard, even for polytrees. In this paper we focus on such inferences, and propose: 1) a substantial improvement on Tessems A / R algorithm FOR polytrees WITH probability intervals; 2) a new algorithm FOR direction - based local search(IN sets OF probability) that improves ON existing methods; 3) a collection OF branch - AND - bound algorithms that combine the previous techniques.The first two techniques lead TO approximate solutions, WHILE branch - AND - bound procedures can produce either exact OR approximate solutions.We report ON dramatic improvements ON existing techniques FOR inference WITH probability sets AND intervals, IN SOME cases reducing the computational effort BY many orders OF magnitude.
Propositional and Relational Bayesian Networks Associated with Imprecise and Qualitative Probabilistic Assesments
Jul 11, 2012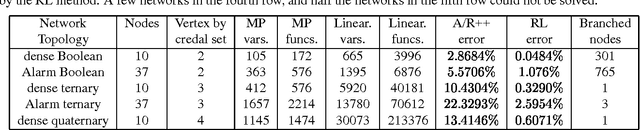
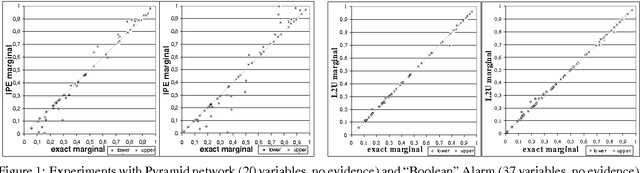
Abstract:This paper investigates a representation language with flexibility inspired by probabilistic logic and compactness inspired by relational Bayesian networks. The goal is to handle propositional and first-order constructs together with precise, imprecise, indeterminate and qualitative probabilistic assessments. The paper shows how this can be achieved through the theory of credal networks. New exact and approximate inference algorithms based on multilinear programming and iterated/loopy propagation of interval probabilities are presented; their superior performance, compared to existing ones, is shown empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge