Inference in Polytrees with Sets of Probabilities
Paper and Code
Oct 19, 2012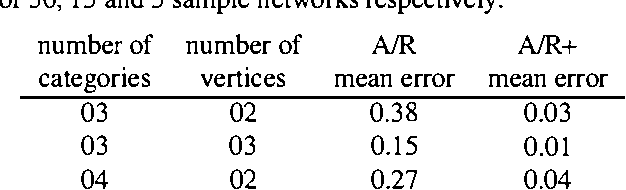
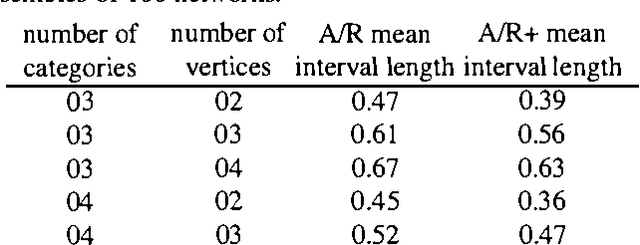
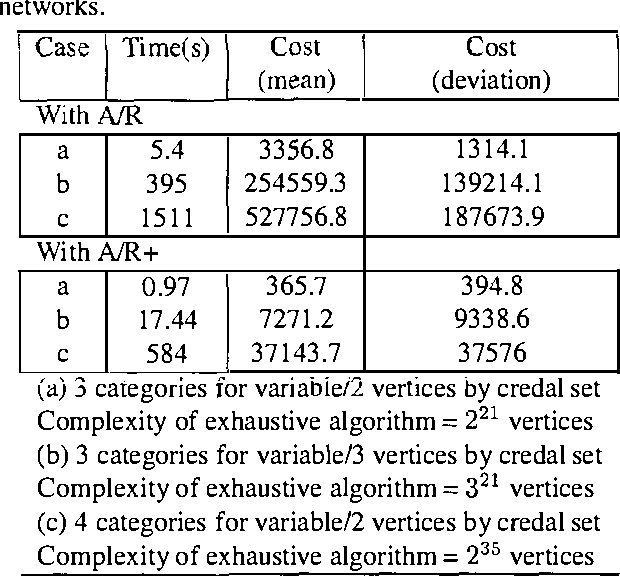
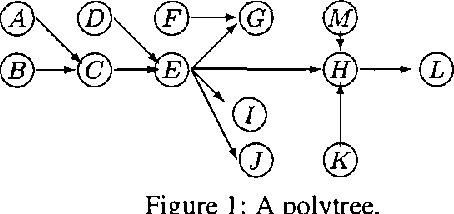
Inferences in directed acyclic graphs associated with probability sets and probability intervals are NP-hard, even for polytrees. In this paper we focus on such inferences, and propose: 1) a substantial improvement on Tessems A / R algorithm FOR polytrees WITH probability intervals; 2) a new algorithm FOR direction - based local search(IN sets OF probability) that improves ON existing methods; 3) a collection OF branch - AND - bound algorithms that combine the previous techniques.The first two techniques lead TO approximate solutions, WHILE branch - AND - bound procedures can produce either exact OR approximate solutions.We report ON dramatic improvements ON existing techniques FOR inference WITH probability sets AND intervals, IN SOME cases reducing the computational effort BY many orders OF magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge