Compiling Stochastic Constraint Programs to And-Or Decision Diagrams

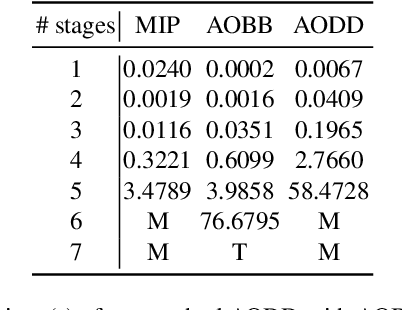
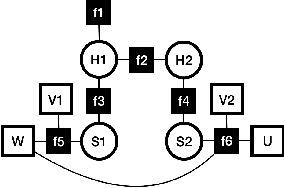
Factored stochastic constraint programming (FSCP) is a formalism to represent multi-stage decision making problems under uncertainty. FSCP models support factorized probabilistic models and involve constraints over decision and random variables. These models have many applications in real-world problems. However, solving these problems requires evaluating the best course of action for each possible outcome of the random variables and hence is computationally challenging. FSCP problems often involve repeated subproblems which ideally should be solved once. In this paper we show how identifying and exploiting these identical subproblems can simplify solving them and leads to a compact representation of the solution. We compile an And-Or search tree to a compact decision diagram. Preliminary experiments show that our proposed method significantly improves the search efficiency by reducing the size of the problem and outperforms the existing methods.

Learning Fair Naive Bayes Classifiers by Discovering and Eliminating Discrimination Patterns

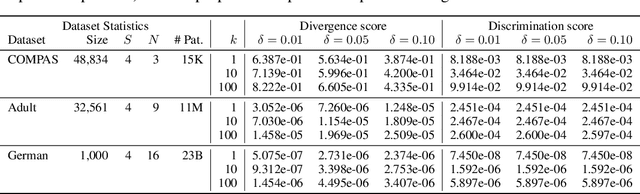
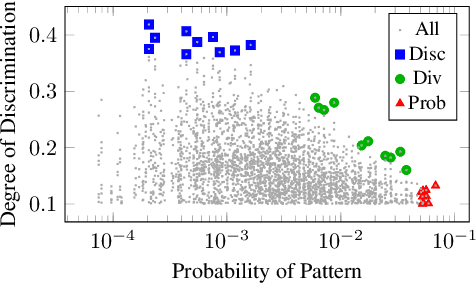
As machine learning is increasingly used to make real-world decisions, recent research efforts aim to define and ensure fairness in algorithmic decision making. Existing methods often assume a fixed set of observable features to define individuals, but lack a discussion of certain features not being observed at test time. In this paper, we study fairness of naive Bayes classifiers, which allow partial observations. In particular, we introduce the notion of a discrimination pattern, which refers to an individual receiving different classifications depending on whether some sensitive attributes were observed. Then a model is considered fair if it has no such pattern. We propose an algorithm to discover and mine for discrimination patterns in a naive Bayes classifier, and show how to learn maximum-likelihood parameters subject to these fairness constraints. Our approach iteratively discovers and eliminates discrimination patterns until a fair model is learned. An empirical evaluation on three real-world datasets demonstrates that we can remove exponentially many discrimination patterns by only adding a small fraction of them as constraints.

Stochastic Constraint Optimization using Propagation on Ordered Binary Decision Diagrams

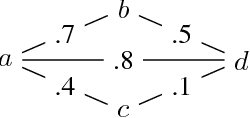
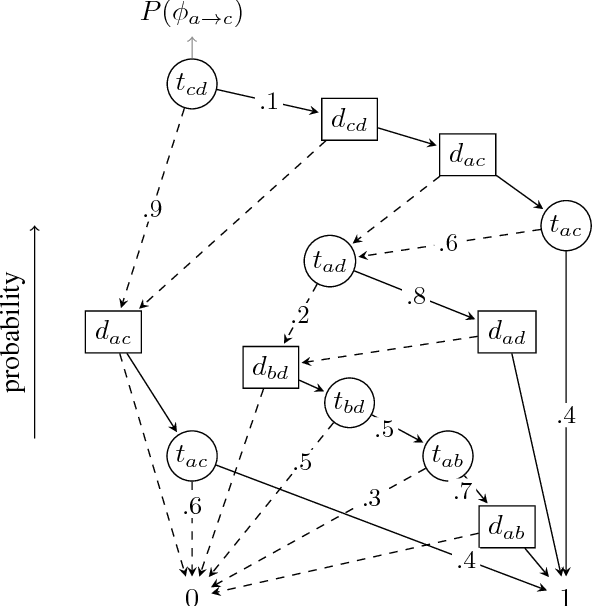
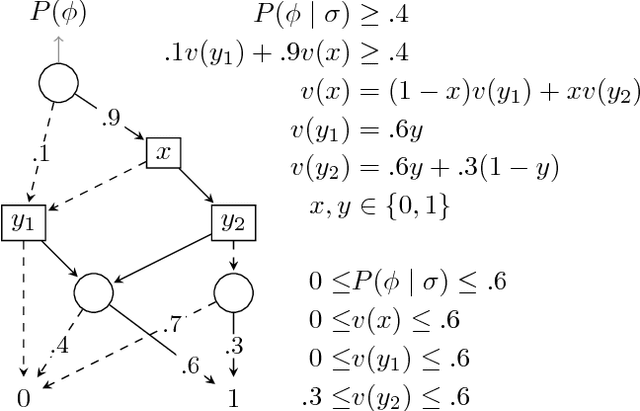
A number of problems in relational Artificial Intelligence can be viewed as Stochastic Constraint Optimization Problems (SCOPs). These are constraint optimization problems that involve objectives or constraints with a stochastic component. Building on the recently proposed language SC-ProbLog for modeling SCOPs, we propose a new method for solving these problems. Earlier methods used Probabilistic Logic Programming (PLP) techniques to create Ordered Binary Decision Diagrams (OBDDs), which were decomposed into smaller constraints in order to exploit existing constraint programming (CP) solvers. We argue that this approach has as drawback that a decomposed representation of an OBDD does not guarantee domain consistency during search, and hence limits the efficiency of the solver. For the specific case of monotonic distributions, we suggest an alternative method for using CP in SCOP, based on the development of a new propagator; we show that this propagator is linear in the size of the OBDD, and has the potential to be more efficient than the decomposition method, as it maintains domain consistency.