Handling Missing Data in Decision Trees: A Probabilistic Approach
Paper and Code
Jun 29, 2020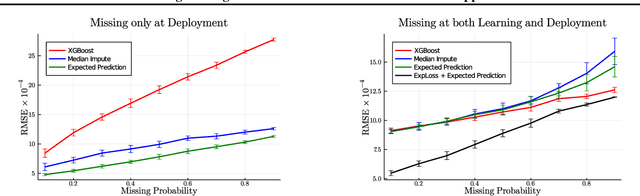

Decision trees are a popular family of models due to their attractive properties such as interpretability and ability to handle heterogeneous data. Concurrently, missing data is a prevalent occurrence that hinders performance of machine learning models. As such, handling missing data in decision trees is a well studied problem. In this paper, we tackle this problem by taking a probabilistic approach. At deployment time, we use tractable density estimators to compute the "expected prediction" of our models. At learning time, we fine-tune parameters of already learned trees by minimizing their "expected prediction loss" w.r.t.\ our density estimators. We provide brief experiments showcasing effectiveness of our methods compared to few baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge