Discrete Copula Diffusion

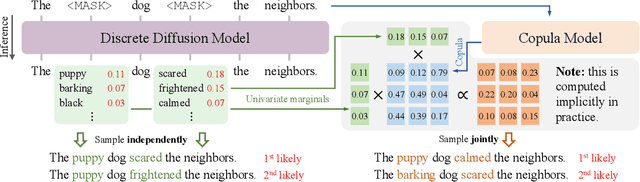
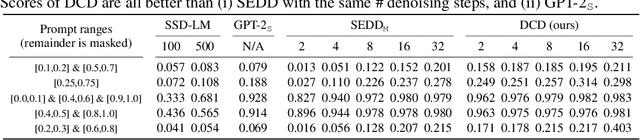
Discrete diffusion models have recently shown significant progress in modeling complex data, such as natural languages and DNA sequences. However, unlike diffusion models for continuous data, which can generate high-quality samples in just a few denoising steps, modern discrete diffusion models still require hundreds or even thousands of denoising steps to perform well. In this paper, we identify a fundamental limitation that prevents discrete diffusion models from achieving strong performance with fewer steps -- they fail to capture dependencies between output variables at each denoising step. To address this issue, we provide a formal explanation and introduce a general approach to supplement the missing dependency information by incorporating another deep generative model, termed the copula model. Our method does not require fine-tuning either the diffusion model or the copula model, yet it enables high-quality sample generation with significantly fewer denoising steps. When we apply this approach to autoregressive copula models, the combined model outperforms both models individually in unconditional and conditional text generation. Specifically, the hybrid model achieves better (un)conditional text generation using 8 to 32 times fewer denoising steps than the diffusion model alone. In addition to presenting an effective discrete diffusion generation algorithm, this paper emphasizes the importance of modeling inter-variable dependencies in discrete diffusion.

Probabilistic Circuits for Cumulative Distribution Functions

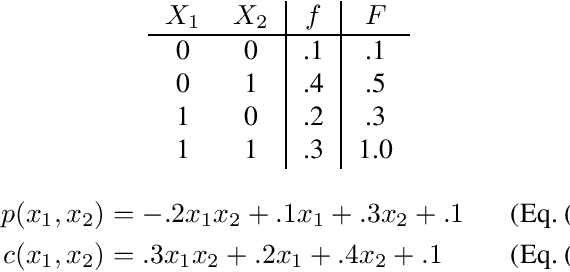
A probabilistic circuit (PC) succinctly expresses a function that represents a multivariate probability distribution and, given sufficient structural properties of the circuit, supports efficient probabilistic inference. Typically a PC computes the probability mass (or density) function (PMF or PDF) of the distribution. We consider PCs instead computing the cumulative distribution function (CDF). We show that for distributions over binary random variables these representations (PMF and CDF) are essentially equivalent, in the sense that one can be transformed to the other in polynomial time. We then show how a similar equivalence holds for distributions over finite discrete variables using a modification of the standard encoding with binary variables that aligns with the CDF semantics. Finally we show that for continuous variables, smooth, decomposable PCs computing PDFs and CDFs can be efficiently transformed to each other by modifying only the leaves of the circuit.

Polynomial Semantics of Tractable Probabilistic Circuits

Probabilistic circuits compute multilinear polynomials that represent probability distributions. They are tractable models that support efficient marginal inference. However, various polynomial semantics have been considered in the literature (e.g., network polynomials, likelihood polynomials, generating functions, Fourier transforms, and characteristic polynomials). The relationships between these polynomial encodings of distributions is largely unknown. In this paper, we prove that for binary distributions, each of these probabilistic circuit models is equivalent in the sense that any circuit for one of them can be transformed into a circuit for any of the others with only a polynomial increase in size. They are therefore all tractable for marginal inference on the same class of distributions. Finally, we explore the natural extension of one such polynomial semantics, called probabilistic generating circuits, to categorical random variables, and establish that marginal inference becomes #P-hard.