Learning to Approximate Particle Smoothing Trajectories via Diffusion Generative Models

Learning dynamical systems from sparse observations is critical in numerous fields, including biology, finance, and physics. Even if tackling such problems is standard in general information fusion, it remains challenging for contemporary machine learning models, such as diffusion models. We introduce a method that integrates conditional particle filtering with ancestral sampling and diffusion models, enabling the generation of realistic trajectories that align with observed data. Our approach uses a smoother based on iterating a conditional particle filter with ancestral sampling to first generate plausible trajectories matching observed marginals, and learns the corresponding diffusion model. This approach provides both a generative method for high-quality, smoothed trajectories under complex constraints, and an efficient approximation of the particle smoothing distribution for classical tracking problems. We demonstrate the approach in time-series generation and interpolation tasks, including vehicle tracking and single-cell RNA sequencing data.

Function-space Parameterization of Neural Networks for Sequential Learning

Sequential learning paradigms pose challenges for gradient-based deep learning due to difficulties incorporating new data and retaining prior knowledge. While Gaussian processes elegantly tackle these problems, they struggle with scalability and handling rich inputs, such as images. To address these issues, we introduce a technique that converts neural networks from weight space to function space, through a dual parameterization. Our parameterization offers: (i) a way to scale function-space methods to large data sets via sparsification, (ii) retention of prior knowledge when access to past data is limited, and (iii) a mechanism to incorporate new data without retraining. Our experiments demonstrate that we can retain knowledge in continual learning and incorporate new data efficiently. We further show its strengths in uncertainty quantification and guiding exploration in model-based RL. Further information and code is available on the project website.

Sparse Function-space Representation of Neural Networks

Deep neural networks (NNs) are known to lack uncertainty estimates and struggle to incorporate new data. We present a method that mitigates these issues by converting NNs from weight space to function space, via a dual parameterization. Importantly, the dual parameterization enables us to formulate a sparse representation that captures information from the entire data set. This offers a compact and principled way of capturing uncertainty and enables us to incorporate new data without retraining whilst retaining predictive performance. We provide proof-of-concept demonstrations with the proposed approach for quantifying uncertainty in supervised learning on UCI benchmark tasks.

Transport with Support: Data-Conditional Diffusion Bridges

The dynamic Schr\"odinger bridge problem provides an appealing setting for solving optimal transport problems by learning non-linear diffusion processes using efficient iterative solvers. Recent works have demonstrated state-of-the-art results (eg. in modelling single-cell embryo RNA sequences or sampling from complex posteriors) but are limited to learning bridges with only initial and terminal constraints. Our work extends this paradigm by proposing the Iterative Smoothing Bridge (ISB). We integrate Bayesian filtering and optimal control into learning the diffusion process, enabling constrained stochastic processes governed by sparse observations at intermediate stages and terminal constraints. We assess the effectiveness of our method on synthetic and real-world data and show that the ISB generalises well to high-dimensional data, is computationally efficient, and provides accurate estimates of the marginals at intermediate and terminal times.

Scalable Inference in SDEs by Direct Matching of the Fokker-Planck-Kolmogorov Equation

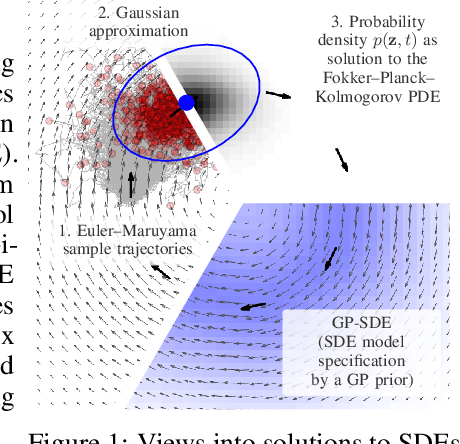
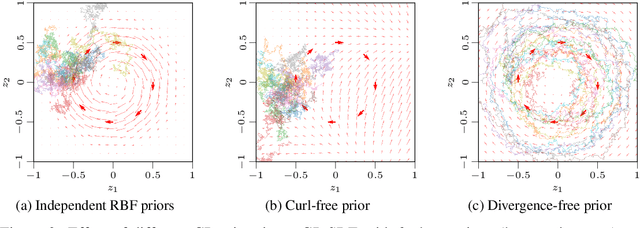
Simulation-based techniques such as variants of stochastic Runge-Kutta are the de facto approach for inference with stochastic differential equations (SDEs) in machine learning. These methods are general-purpose and used with parametric and non-parametric models, and neural SDEs. Stochastic Runge-Kutta relies on the use of sampling schemes that can be inefficient in high dimensions. We address this issue by revisiting the classical SDE literature and derive direct approximations to the (typically intractable) Fokker-Planck-Kolmogorov equation by matching moments. We show how this workflow is fast, scales to high-dimensional latent spaces, and is applicable to scarce-data applications, where a non-parametric SDE with a driving Gaussian process velocity field specifies the model.