Contextual Latent World Models for Offline Meta Reinforcement Learning

Offline meta-reinforcement learning seeks to learn policies that generalize across related tasks from fixed datasets. Context-based methods infer a task representation from transition histories, but learning effective task representations without supervision remains a challenge. In parallel, latent world models have demonstrated strong self-supervised representation learning through temporal consistency. We introduce contextual latent world models, which condition latent world models on inferred task representations and train them jointly with the context encoder. This enforces task-conditioned temporal consistency, yielding task representations that capture task-dependent dynamics rather than merely discriminating between tasks. Our method learns more expressive task representations and significantly improves generalization to unseen tasks across MuJoCo, Contextual-DeepMind Control, and Meta-World benchmarks.

Kalman Linear Attention: Parallel Bayesian Filtering For Efficient Language Modelling and State Tracking

State-space language models such as Mamba and gated linear attention (GLA) offer efficient alternatives to transformers due to their linear complexity and parallel training, but often lack the expressivity and robust state-tracking needed for complex reasoning. We address these limitations by reframing sequence modelling through a probabilistic lens, using Bayesian filters as a core primitive. While classical filters such as Kalman filters provide principled state estimation and uncertainty tracking, they are typically viewed as inherently sequential. We show that reparameterising the Kalman filter in information form enables its updates to be computed via an associative scan, allowing efficient parallel training. Building on this insight, we introduce the Kalman Linear Attention (KLA) layer, a neural sequence-modelling primitive that performs time-parallel probabilistic inference while maintaining explicit belief-state uncertainty. KLA offers strictly more expressive nonlinear updates and gating than GLA variants while retaining their computational advantages. On language modelling tasks, KLA matches or outperforms modern SSMs and GLAs across representative discrete token-manipulation and state-tracking benchmarks.

Forgetting is Everywhere

A fundamental challenge in developing general learning algorithms is their tendency to forget past knowledge when adapting to new data. Addressing this problem requires a principled understanding of forgetting; yet, despite decades of study, no unified definition has emerged that provides insights into the underlying dynamics of learning. We propose an algorithm- and task-agnostic theory that characterises forgetting as a lack of self-consistency in a learner's predictive distribution over future experiences, manifesting as a loss of predictive information. Our theory naturally yields a general measure of an algorithm's propensity to forget. To validate the theory, we design a comprehensive set of experiments that span classification, regression, generative modelling, and reinforcement learning. We empirically demonstrate how forgetting is present across all learning settings and plays a significant role in determining learning efficiency. Together, these results establish a principled understanding of forgetting and lay the foundation for analysing and improving the information retention capabilities of general learning algorithms.

Generative World Modelling for Humanoids: 1X World Model Challenge Technical Report

World models are a powerful paradigm in AI and robotics, enabling agents to reason about the future by predicting visual observations or compact latent states. The 1X World Model Challenge introduces an open-source benchmark of real-world humanoid interaction, with two complementary tracks: sampling, focused on forecasting future image frames, and compression, focused on predicting future discrete latent codes. For the sampling track, we adapt the video generation foundation model Wan-2.2 TI2V-5B to video-state-conditioned future frame prediction. We condition the video generation on robot states using AdaLN-Zero, and further post-train the model using LoRA. For the compression track, we train a Spatio-Temporal Transformer model from scratch. Our models achieve 23.0 dB PSNR in the sampling task and a Top-500 CE of 6.6386 in the compression task, securing 1st place in both challenges.

Generalist World Model Pre-Training for Efficient Reinforcement Learning

Sample-efficient robot learning is a longstanding goal in robotics. Inspired by the success of scaling in vision and language, the robotics community is now investigating large-scale offline datasets for robot learning. However, existing methods often require expert and/or reward-labeled task-specific data, which can be costly and limit their application in practice. In this paper, we consider a more realistic setting where the offline data consists of reward-free and non-expert multi-embodiment offline data. We show that generalist world model pre-training (WPT), together with retrieval-based experience rehearsal and execution guidance, enables efficient reinforcement learning (RL) and fast task adaptation with such non-curated data. In experiments over 72 visuomotor tasks, spanning 6 different embodiments, covering hard exploration, complex dynamics, and various visual properties, WPT achieves 35.65% and 35% higher aggregated score compared to widely used learning-from-scratch baselines, respectively.

Entropy Regularized Task Representation Learning for Offline Meta-Reinforcement Learning

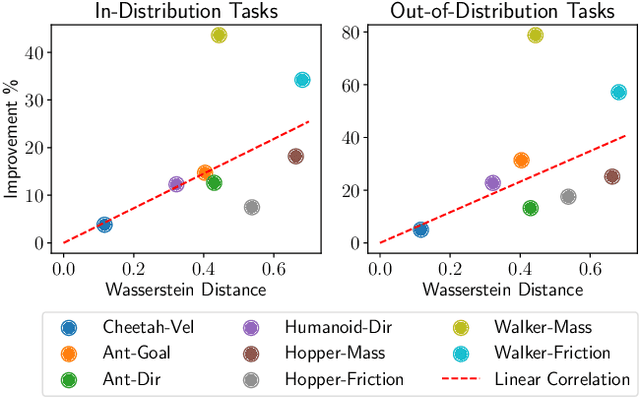
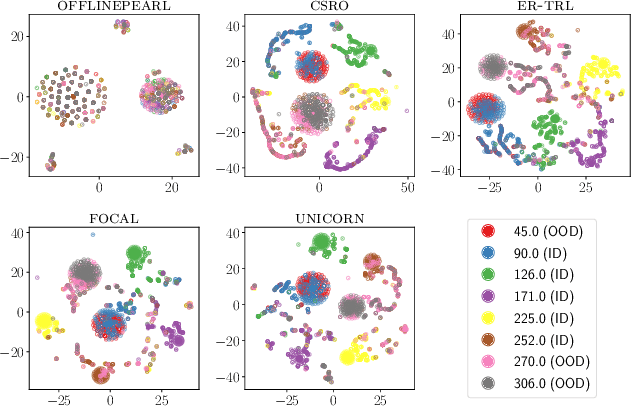
Offline meta-reinforcement learning aims to equip agents with the ability to rapidly adapt to new tasks by training on data from a set of different tasks. Context-based approaches utilize a history of state-action-reward transitions -- referred to as the context -- to infer representations of the current task, and then condition the agent, i.e., the policy and value function, on the task representations. Intuitively, the better the task representations capture the underlying tasks, the better the agent can generalize to new tasks. Unfortunately, context-based approaches suffer from distribution mismatch, as the context in the offline data does not match the context at test time, limiting their ability to generalize to the test tasks. This leads to the task representations overfitting to the offline training data. Intuitively, the task representations should be independent of the behavior policy used to collect the offline data. To address this issue, we approximately minimize the mutual information between the distribution over the task representations and behavior policy by maximizing the entropy of behavior policy conditioned on the task representations. We validate our approach in MuJoCo environments, showing that compared to baselines, our task representations more faithfully represent the underlying tasks, leading to outperforming prior methods in both in-distribution and out-of-distribution tasks.

Residual Learning and Context Encoding for Adaptive Offline-to-Online Reinforcement Learning

Offline reinforcement learning (RL) allows learning sequential behavior from fixed datasets. Since offline datasets do not cover all possible situations, many methods collect additional data during online fine-tuning to improve performance. In general, these methods assume that the transition dynamics remain the same during both the offline and online phases of training. However, in many real-world applications, such as outdoor construction and navigation over rough terrain, it is common for the transition dynamics to vary between the offline and online phases. Moreover, the dynamics may vary during the online fine-tuning. To address this problem of changing dynamics from offline to online RL we propose a residual learning approach that infers dynamics changes to correct the outputs of the offline solution. At the online fine-tuning phase, we train a context encoder to learn a representation that is consistent inside the current online learning environment while being able to predict dynamic transitions. Experiments in D4RL MuJoCo environments, modified to support dynamics' changes upon environment resets, show that our approach can adapt to these dynamic changes and generalize to unseen perturbations in a sample-efficient way, whilst comparison methods cannot.

iQRL -- Implicitly Quantized Representations for Sample-efficient Reinforcement Learning

Learning representations for reinforcement learning (RL) has shown much promise for continuous control. We propose an efficient representation learning method using only a self-supervised latent-state consistency loss. Our approach employs an encoder and a dynamics model to map observations to latent states and predict future latent states, respectively. We achieve high performance and prevent representation collapse by quantizing the latent representation such that the rank of the representation is empirically preserved. Our method, named iQRL: implicitly Quantized Reinforcement Learning, is straightforward, compatible with any model-free RL algorithm, and demonstrates excellent performance by outperforming other recently proposed representation learning methods in continuous control benchmarks from DeepMind Control Suite.

Function-space Parameterization of Neural Networks for Sequential Learning

Sequential learning paradigms pose challenges for gradient-based deep learning due to difficulties incorporating new data and retaining prior knowledge. While Gaussian processes elegantly tackle these problems, they struggle with scalability and handling rich inputs, such as images. To address these issues, we introduce a technique that converts neural networks from weight space to function space, through a dual parameterization. Our parameterization offers: (i) a way to scale function-space methods to large data sets via sparsification, (ii) retention of prior knowledge when access to past data is limited, and (iii) a mechanism to incorporate new data without retraining. Our experiments demonstrate that we can retain knowledge in continual learning and incorporate new data efficiently. We further show its strengths in uncertainty quantification and guiding exploration in model-based RL. Further information and code is available on the project website.

Sparse Function-space Representation of Neural Networks

Deep neural networks (NNs) are known to lack uncertainty estimates and struggle to incorporate new data. We present a method that mitigates these issues by converting NNs from weight space to function space, via a dual parameterization. Importantly, the dual parameterization enables us to formulate a sparse representation that captures information from the entire data set. This offers a compact and principled way of capturing uncertainty and enables us to incorporate new data without retraining whilst retaining predictive performance. We provide proof-of-concept demonstrations with the proposed approach for quantifying uncertainty in supervised learning on UCI benchmark tasks.