ABM-UDE: Developing Surrogates for Epidemic Agent-Based Models via Scientific Machine Learning

Agent-based epidemic models (ABMs) encode behavioral and policy heterogeneity but are too slow for nightly hospital planning. We develop county-ready surrogates that learn directly from exascale ABM trajectories using Universal Differential Equations (UDEs): mechanistic SEIR-family ODEs with a neural-parameterized contact rate $κ_φ(u,t)$ (no additive residual). Our contributions are threefold: we adapt multiple shooting and an observer-based prediction-error method (PEM) to stabilize identification of neural-augmented epidemiological dynamics across intervention-driven regime shifts; we enforce positivity and mass conservation and show the learned contact-rate parameterization yields a well-posed vector field; and we quantify accuracy, calibration, and compute against ABM ensembles and UDE baselines. On a representative ExaEpi scenario, PEM-UDE reduces mean MSE by 77% relative to single-shooting UDE (3.00 vs. 13.14) and by 20% relative to MS-UDE (3.75). Reliability improves in parallel: empirical coverage of ABM $10$-$90$% and $25$-$75$% bands rises from 0.68/0.43 (UDE) and 0.79/0.55 (MS-UDE) to 0.86/0.61 with PEM-UDE and 0.94/0.69 with MS+PEM-UDE, indicating calibrated uncertainty rather than overconfident fits. Inference runs in seconds on commodity CPUs (20-35 s per $\sim$90-day forecast), enabling nightly ''what-if'' sweeps on a laptop. Relative to a $\sim$100 CPU-hour ABM reference run, this yields $\sim10^{4}\times$ lower wall-clock per scenario. This closes the realism-cadence gap, supports threshold-aware decision-making (e.g., maintaining ICU occupancy $<75$%), preserves mechanistic interpretability, and enables calibrated, risk-aware scenario planning on standard institutional hardware. Beyond epidemics, the ABM$\to$UDE recipe provides a portable path to distill agent-based simulators into fast, trustworthy surrogates for other scientific domains.

Physics-Constrained Flow Matching: Sampling Generative Models with Hard Constraints

Deep generative models have recently been applied to physical systems governed by partial differential equations (PDEs), offering scalable simulation and uncertainty-aware inference. However, enforcing physical constraints, such as conservation laws (linear and nonlinear) and physical consistencies, remains challenging. Existing methods often rely on soft penalties or architectural biases that fail to guarantee hard constraints. In this work, we propose Physics-Constrained Flow Matching (PCFM), a zero-shot inference framework that enforces arbitrary nonlinear constraints in pretrained flow-based generative models. PCFM continuously guides the sampling process through physics-based corrections applied to intermediate solution states, while remaining aligned with the learned flow and satisfying physical constraints. Empirically, PCFM outperforms both unconstrained and constrained baselines on a range of PDEs, including those with shocks, discontinuities, and sharp features, while ensuring exact constraint satisfaction at the final solution. Our method provides a general framework for enforcing hard constraints in both scientific and general-purpose generative models, especially in applications where constraint satisfaction is essential.

Semi-Explicit Neural DAEs: Learning Long-Horizon Dynamical Systems with Algebraic Constraints

Despite the promise of scientific machine learning (SciML) in combining data-driven techniques with mechanistic modeling, existing approaches for incorporating hard constraints in neural differential equations (NDEs) face significant limitations. Scalability issues and poor numerical properties prevent these neural models from being used for modeling physical systems with complicated conservation laws. We propose Manifold-Projected Neural ODEs (PNODEs), a method that explicitly enforces algebraic constraints by projecting each ODE step onto the constraint manifold. This framework arises naturally from semi-explicit differential-algebraic equations (DAEs), and includes both a robust iterative variant and a fast approximation requiring a single Jacobian factorization. We further demonstrate that prior works on relaxation methods are special cases of our approach. PNODEs consistently outperform baselines across six benchmark problems achieving a mean constraint violation error below $10^{-10}$. Additionally, PNODEs consistently achieve lower runtime compared to other methods for a given level of error tolerance. These results show that constraint projection offers a simple strategy for learning physically consistent long-horizon dynamics.

Locally Regularized Neural Differential Equations: Some Black Boxes Were Meant to Remain Closed!

Implicit layer deep learning techniques, like Neural Differential Equations, have become an important modeling framework due to their ability to adapt to new problems automatically. Training a neural differential equation is effectively a search over a space of plausible dynamical systems. However, controlling the computational cost for these models is difficult since it relies on the number of steps the adaptive solver takes. Most prior works have used higher-order methods to reduce prediction timings while greatly increasing training time or reducing both training and prediction timings by relying on specific training algorithms, which are harder to use as a drop-in replacement due to strict requirements on automatic differentiation. In this manuscript, we use internal cost heuristics of adaptive differential equation solvers at stochastic time points to guide the training toward learning a dynamical system that is easier to integrate. We "close the black-box" and allow the use of our method with any adjoint technique for gradient calculations of the differential equation solution. We perform experimental studies to compare our method to global regularization to show that we attain similar performance numbers without compromising the flexibility of implementation on ordinary differential equations (ODEs) and stochastic differential equations (SDEs). We develop two sampling strategies to trade off between performance and training time. Our method reduces the number of function evaluations to 0.556-0.733x and accelerates predictions by 1.3-2x.

Mixing Implicit and Explicit Deep Learning with Skip DEQs and Infinite Time Neural ODEs (Continuous DEQs)

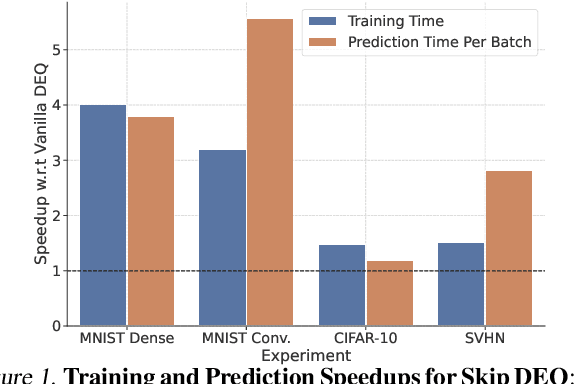
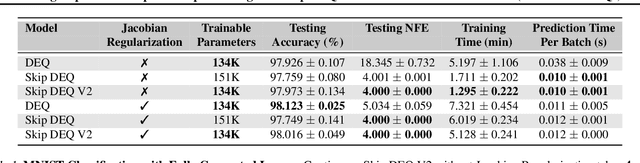
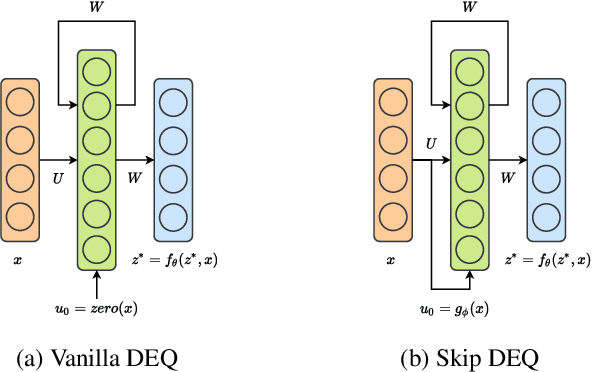
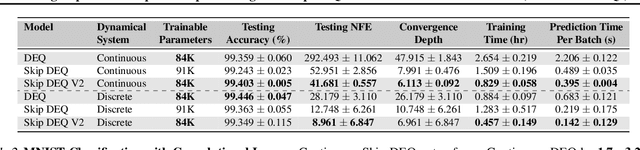
Implicit deep learning architectures, like Neural ODEs and Deep Equilibrium Models (DEQs), separate the definition of a layer from the description of its solution process. While implicit layers allow features such as depth to adapt to new scenarios and inputs automatically, this adaptivity makes its computational expense challenging to predict. Numerous authors have noted that implicit layer techniques can be more computationally intensive than explicit layer methods. In this manuscript, we address the question: is there a way to simultaneously achieve the robustness of implicit layers while allowing the reduced computational expense of an explicit layer? To solve this we develop Skip DEQ, an implicit-explicit (IMEX) layer that simultaneously trains an explicit prediction followed by an implicit correction. We show that training this explicit layer is free and even decreases the training time by 2.5x and prediction time by 3.4x. We then further increase the "implicitness" of the DEQ by redefining the method in terms of an infinite time neural ODE which paradoxically decreases the training cost over a standard neural ODE by not requiring backpropagation through time. We demonstrate how the resulting Continuous Skip DEQ architecture trains more robustly than the original DEQ while achieving faster training and prediction times. Together, this manuscript shows how bridging the dichotomy of implicit and explicit deep learning can combine the advantages of both techniques.

High-performance symbolic-numerics via multiple dispatch

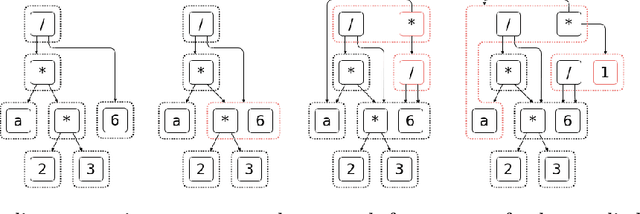
As mathematical computing becomes more democratized in high-level languages, high-performance symbolic-numeric systems are necessary for domain scientists and engineers to get the best performance out of their machine without deep knowledge of code optimization. Naturally, users need different term types either to have different algebraic properties for them, or to use efficient data structures. To this end, we developed Symbolics.jl, an extendable symbolic system which uses dynamic multiple dispatch to change behavior depending on the domain needs. In this work we detail an underlying abstract term interface which allows for speed without sacrificing generality. We show that by formalizing a generic API on actions independent of implementation, we can retroactively add optimized data structures to our system without changing the pre-existing term rewriters. We showcase how this can be used to optimize term construction and give a 113x acceleration on general symbolic transformations. Further, we show that such a generic API allows for complementary term-rewriting implementations. We demonstrate the ability to swap between classical term-rewriting simplifiers and e-graph-based term-rewriting simplifiers. We showcase an e-graph ruleset which minimizes the number of CPU cycles during expression evaluation, and demonstrate how it simplifies a real-world reaction-network simulation to halve the runtime. Additionally, we show a reaction-diffusion partial differential equation solver which is able to be automatically converted into symbolic expressions via multiple dispatch tracing, which is subsequently accelerated and parallelized to give a 157x simulation speedup. Together, this presents Symbolics.jl as a next-generation symbolic-numeric computing environment geared towards modeling and simulation.

ACED: Accelerated Computational Electrochemical systems Discovery

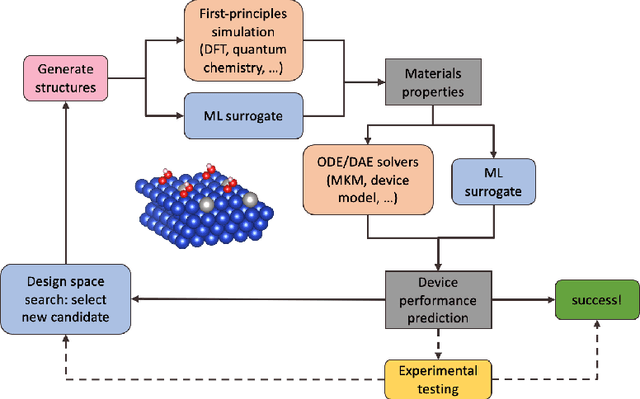
Large-scale electrification is vital to addressing the climate crisis, but many engineering challenges remain to fully electrifying both the chemical industry and transportation. In both of these areas, new electrochemical materials and systems will be critical, but developing these systems currently relies heavily on computationally expensive first-principles simulations as well as human-time-intensive experimental trial and error. We propose to develop an automated workflow that accelerates these computational steps by introducing both automated error handling in generating the first-principles training data as well as physics-informed machine learning surrogates to further reduce computational cost. It will also have the capacity to include automated experiments "in the loop" in order to dramatically accelerate the overall materials discovery pipeline.

Accelerating Simulation of Stiff Nonlinear Systems using Continuous-Time Echo State Networks

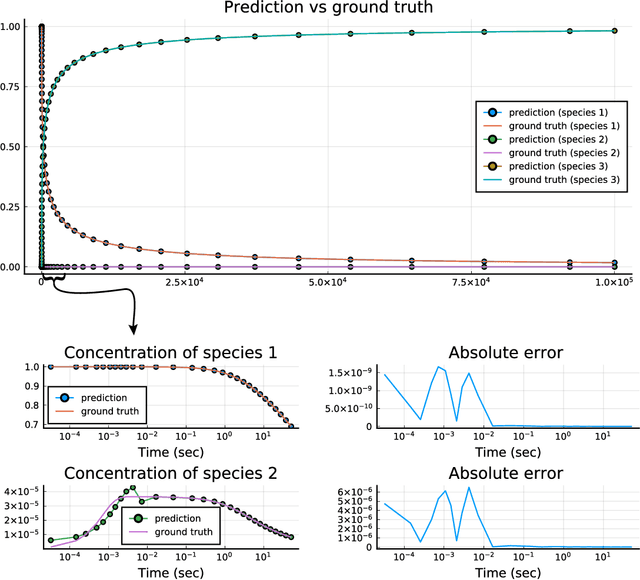
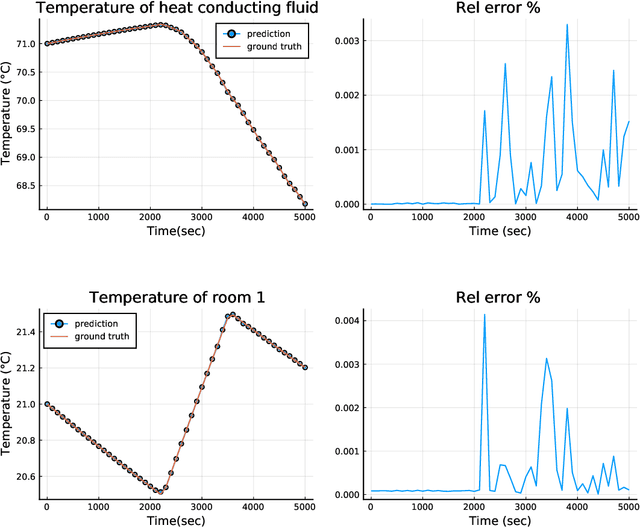
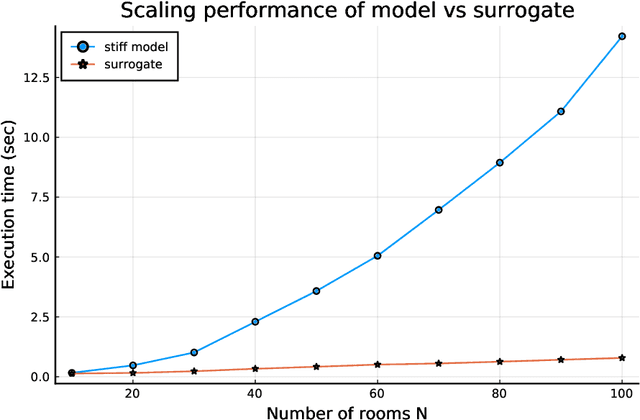
Modern design, control, and optimization often requires simulation of highly nonlinear models, leading to prohibitive computational costs. These costs can be amortized by evaluating a cheap surrogate of the full model. Here we present a general data-driven method, the continuous-time echo state network (CTESN), for generating surrogates of nonlinear ordinary differential equations with dynamics at widely separated timescales. We empirically demonstrate near-constant time performance using our CTESNs on a physically motivated scalable model of a heating system whose full execution time increases exponentially, while maintaining relative error of within 0.2 %. We also show that our model captures fast transients as well as slow dynamics effectively, while other techniques such as physics informed neural networks have difficulties trying to train and predict the highly nonlinear behavior of these models.

Signal Enhancement for Magnetic Navigation Challenge Problem

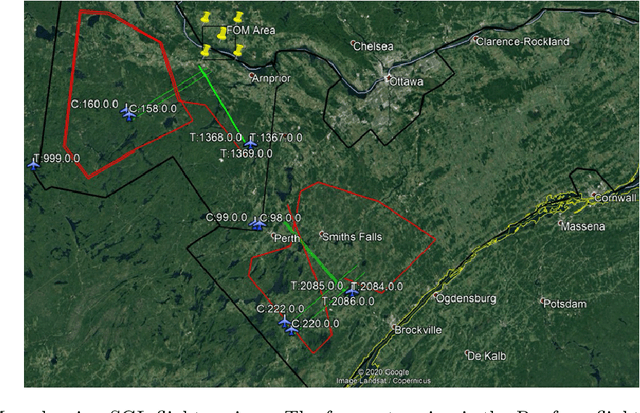
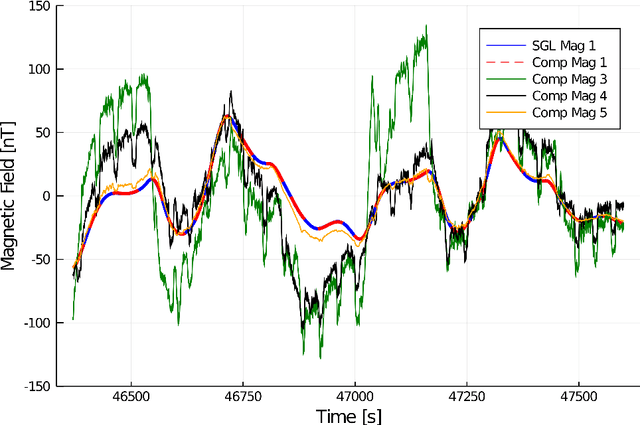
Harnessing the magnetic field of the earth for navigation has shown promise as a viable alternative to other navigation systems. A magnetic navigation system collects its own magnetic field data using a magnetometer and uses magnetic anomaly maps to determine the current location. The greatest challenge with magnetic navigation arises when the magnetic field data from the magnetometer on the navigation system encompass the magnetic field from not just the earth, but also from the vehicle on which it is mounted. It is difficult to separate the earth magnetic anomaly field magnitude, which is crucial for navigation, from the total magnetic field magnitude reading from the sensor. The purpose of this challenge problem is to decouple the earth and aircraft magnetic signals in order to derive a clean signal from which to perform magnetic navigation. Baseline testing on the dataset shows that the earth magnetic field can be extracted from the total magnetic field using machine learning (ML). The challenge is to remove the aircraft magnetic field from the total magnetic field using a trained neural network. These challenges offer an opportunity to construct an effective neural network for removing the aircraft magnetic field from the dataset, using an ML algorithm integrated with physics of magnetic navigation.

A Differentiable Programming System to Bridge Machine Learning and Scientific Computing

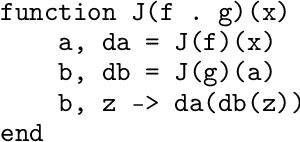
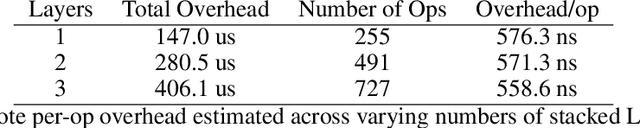
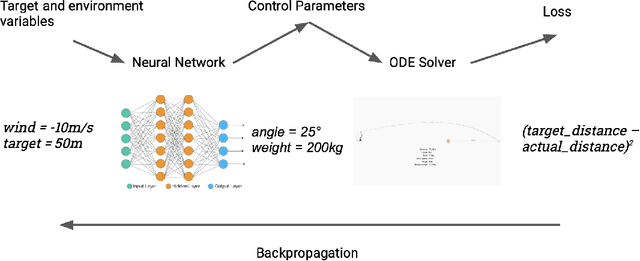
Scientific computing is increasingly incorporating the advancements in machine learning and the ability to work with large amounts of data. At the same time, machine learning models are becoming increasingly sophisticated and exhibit many features often seen in scientific computing, stressing the capabilities of machine learning frameworks. Just as the disciplines of scientific computing and machine learning have shared common underlying infrastructure in the form of numerical linear algebra, we now have the opportunity to further share new computational infrastructure, and thus ideas, in the form of Differentiable Programming. We describe Zygote, a Differentiable Programming system that is able to take gradients of general program structures. We implement this system in the Julia programming language. Our system supports almost all language constructs (control flow, recursion, mutation, etc.) and compiles high-performance code without requiring any user intervention or refactoring to stage computations. This enables an expressive programming model for deep learning, but more importantly, it enables us to incorporate a large ecosystem of libraries in our models in a straightforward way. We discuss our approach to automatic differentiation, including its support for advanced techniques such as mixed-mode, complex and checkpointed differentiation, and present several examples of differentiating programs.