Chris Laughman
Accelerating Simulation of Stiff Nonlinear Systems using Continuous-Time Echo State Networks
Oct 19, 2020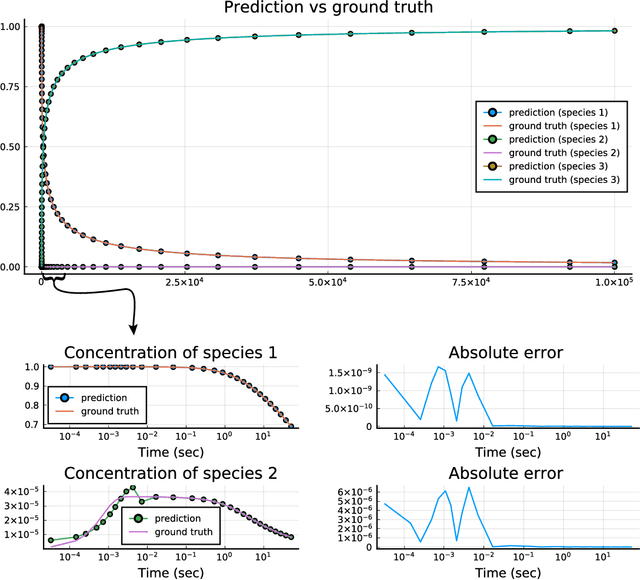
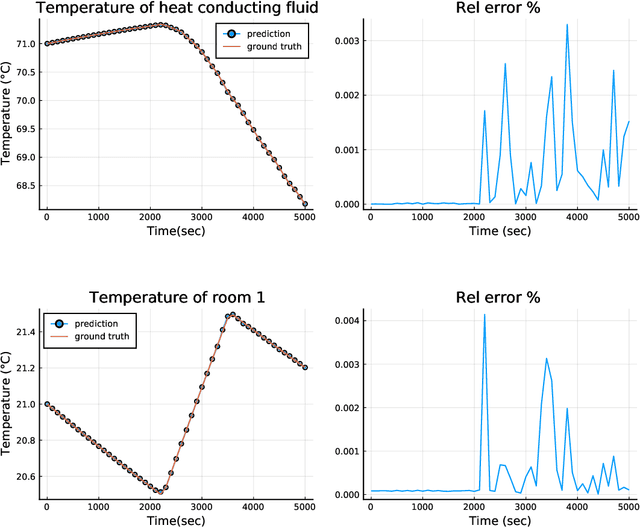

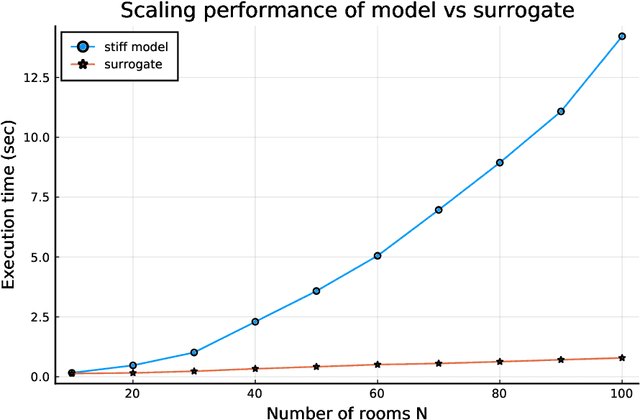
Abstract:Modern design, control, and optimization often requires simulation of highly nonlinear models, leading to prohibitive computational costs. These costs can be amortized by evaluating a cheap surrogate of the full model. Here we present a general data-driven method, the continuous-time echo state network (CTESN), for generating surrogates of nonlinear ordinary differential equations with dynamics at widely separated timescales. We empirically demonstrate near-constant time performance using our CTESNs on a physically motivated scalable model of a heating system whose full execution time increases exponentially, while maintaining relative error of within 0.2 %. We also show that our model captures fast transients as well as slow dynamics effectively, while other techniques such as physics informed neural networks have difficulties trying to train and predict the highly nonlinear behavior of these models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge