Opening the Blackbox: Accelerating Neural Differential Equations by Regularizing Internal Solver Heuristics

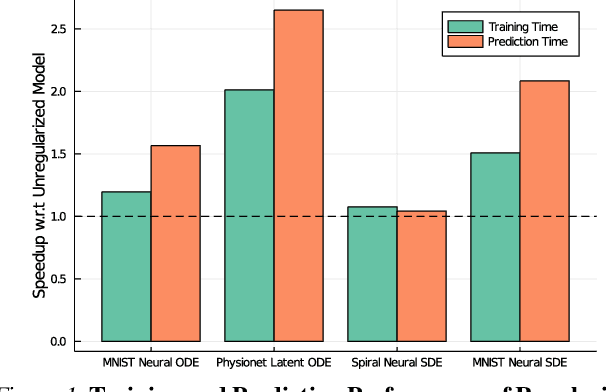
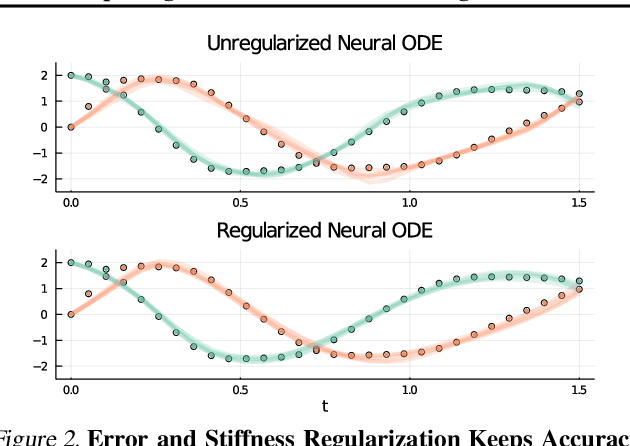
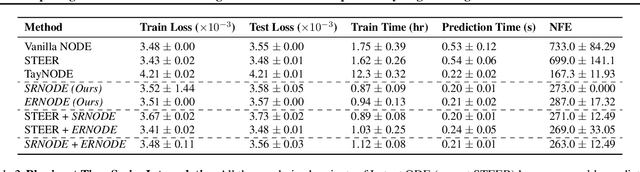
Democratization of machine learning requires architectures that automatically adapt to new problems. Neural Differential Equations (NDEs) have emerged as a popular modeling framework by removing the need for ML practitioners to choose the number of layers in a recurrent model. While we can control the computational cost by choosing the number of layers in standard architectures, in NDEs the number of neural network evaluations for a forward pass can depend on the number of steps of the adaptive ODE solver. But, can we force the NDE to learn the version with the least steps while not increasing the training cost? Current strategies to overcome slow prediction require high order automatic differentiation, leading to significantly higher training time. We describe a novel regularization method that uses the internal cost heuristics of adaptive differential equation solvers combined with discrete adjoint sensitivities to guide the training process towards learning NDEs that are easier to solve. This approach opens up the blackbox numerical analysis behind the differential equation solver's algorithm and directly uses its local error estimates and stiffness heuristics as cheap and accurate cost estimates. We incorporate our method without any change in the underlying NDE framework and show that our method extends beyond Ordinary Differential Equations to accommodate Neural Stochastic Differential Equations. We demonstrate how our approach can halve the prediction time and, unlike other methods which can increase the training time by an order of magnitude, we demonstrate similar reduction in training times. Together this showcases how the knowledge embedded within state-of-the-art equation solvers can be used to enhance machine learning.

ACED: Accelerated Computational Electrochemical systems Discovery

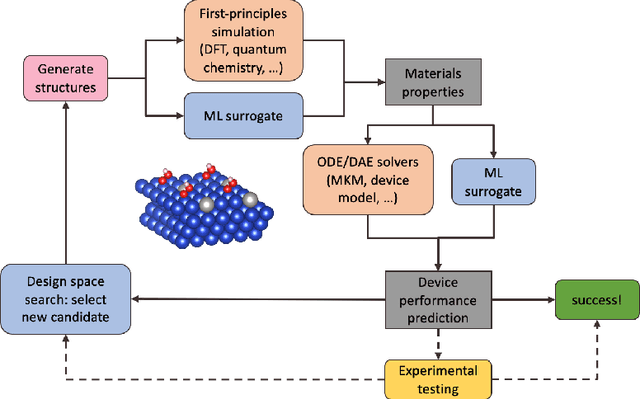
Large-scale electrification is vital to addressing the climate crisis, but many engineering challenges remain to fully electrifying both the chemical industry and transportation. In both of these areas, new electrochemical materials and systems will be critical, but developing these systems currently relies heavily on computationally expensive first-principles simulations as well as human-time-intensive experimental trial and error. We propose to develop an automated workflow that accelerates these computational steps by introducing both automated error handling in generating the first-principles training data as well as physics-informed machine learning surrogates to further reduce computational cost. It will also have the capacity to include automated experiments "in the loop" in order to dramatically accelerate the overall materials discovery pipeline.

Accelerating Simulation of Stiff Nonlinear Systems using Continuous-Time Echo State Networks

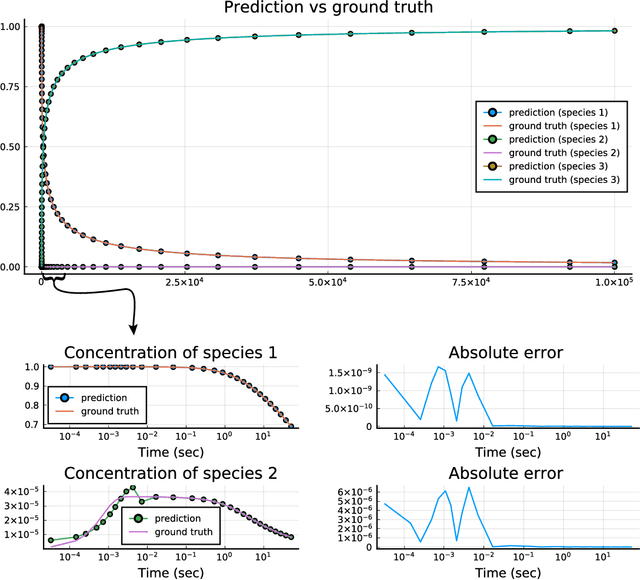
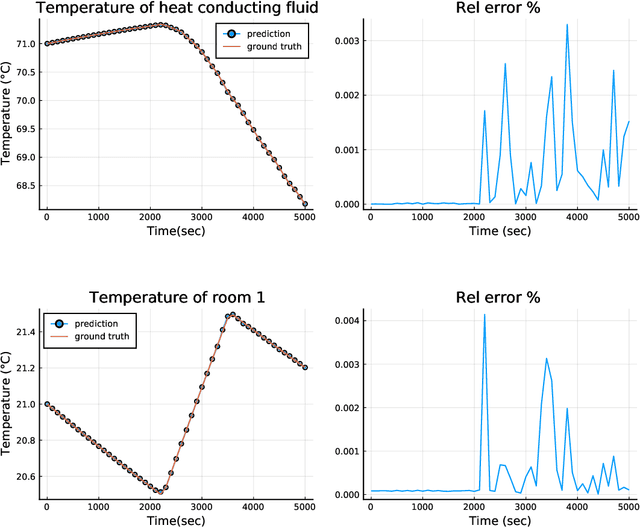
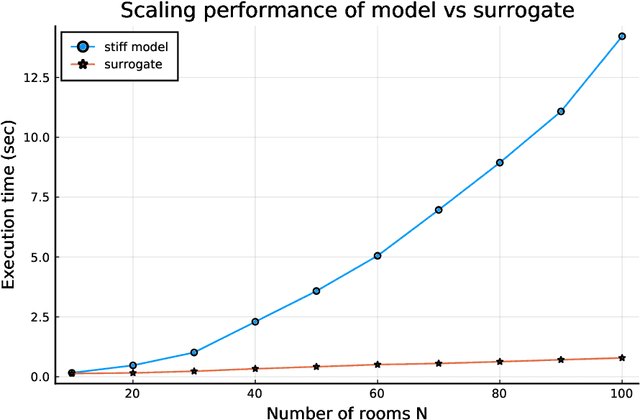
Modern design, control, and optimization often requires simulation of highly nonlinear models, leading to prohibitive computational costs. These costs can be amortized by evaluating a cheap surrogate of the full model. Here we present a general data-driven method, the continuous-time echo state network (CTESN), for generating surrogates of nonlinear ordinary differential equations with dynamics at widely separated timescales. We empirically demonstrate near-constant time performance using our CTESNs on a physically motivated scalable model of a heating system whose full execution time increases exponentially, while maintaining relative error of within 0.2 %. We also show that our model captures fast transients as well as slow dynamics effectively, while other techniques such as physics informed neural networks have difficulties trying to train and predict the highly nonlinear behavior of these models.

Fashionable Modelling with Flux

Machine learning as a discipline has seen an incredible surge of interest in recent years due in large part to a perfect storm of new theory, superior tooling, renewed interest in its capabilities. We present in this paper a framework named Flux that shows how further refinement of the core ideas of machine learning, built upon the foundation of the Julia programming language, can yield an environment that is simple, easily modifiable, and performant. We detail the fundamental principles of Flux as a framework for differentiable programming, give examples of models that are implemented within Flux to display many of the language and framework-level features that contribute to its ease of use and high productivity, display internal compiler techniques used to enable the acceleration and performance that lies at the heart of Flux, and finally give an overview of the larger ecosystem that Flux fits inside of.