End-to-End Optimization of Metasurfaces for Imaging with Compressed Sensing

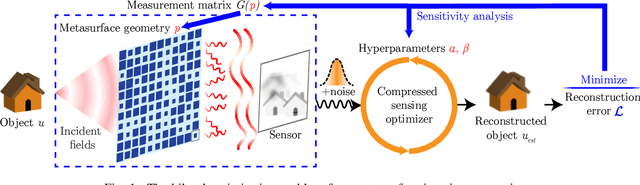
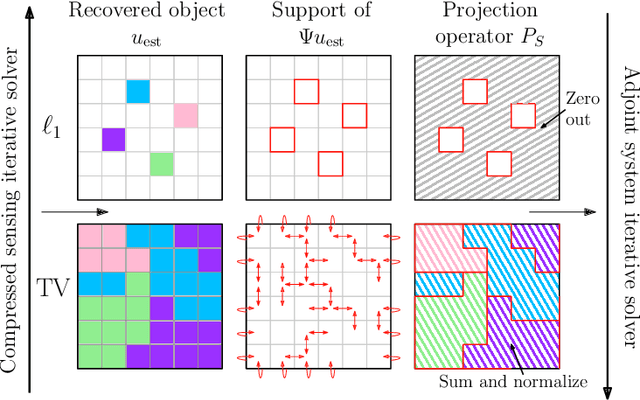
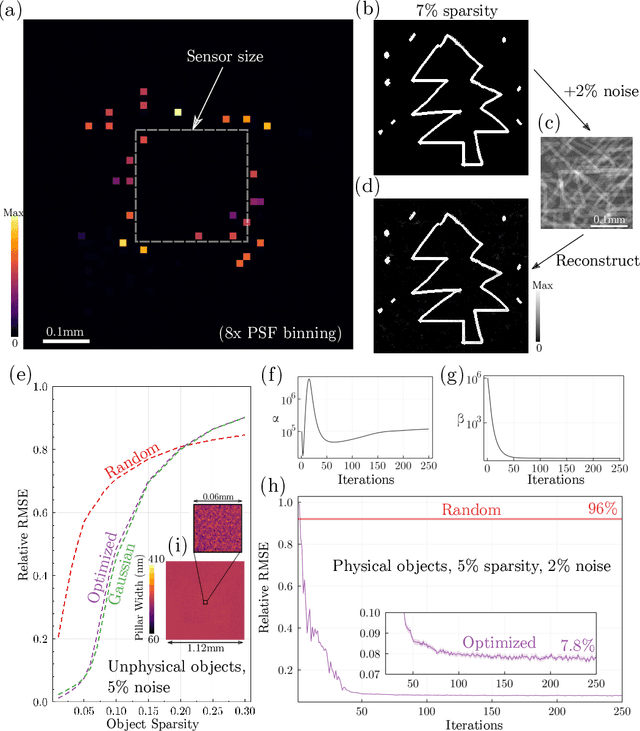
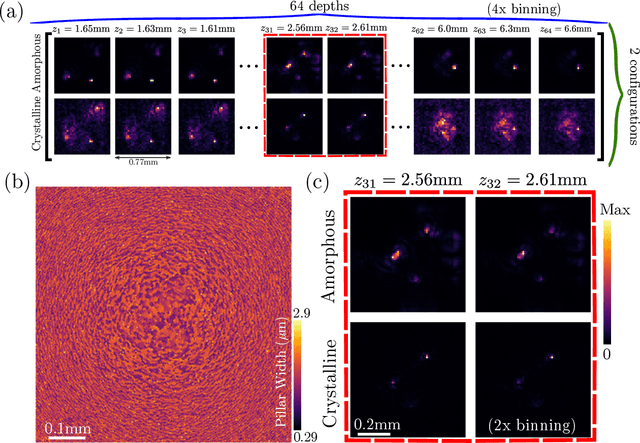
We present a method for the end-to-end optimization of computational imaging systems that reconstruct targets using compressed sensing. Using an adjoint analysis of the Karush-Kuhn-Tucker conditions, we incorporate a fully iterative compressed sensing algorithm that solves an $\ell_1$-regularized minimization problem, nested within the end-to-end optimization pipeline. We apply this method to jointly optimize the optical and computational parameters of metasurface-based imaging systems for underdetermined recovery problems. This allows us to investigate the interplay of nanoscale optics with the design goals of compressed sensing imaging systems. Our optimized metasurface imaging systems are robust to noise, significantly improving over random scattering surfaces and approaching the ideal compressed sensing performance of a Gaussian matrix.