Control of Stochastic Quantum Dynamics with Differentiable Programming
Paper and Code
Jan 04, 2021
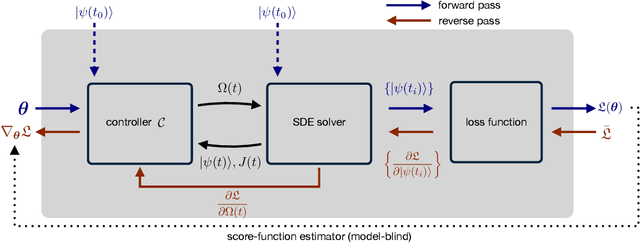

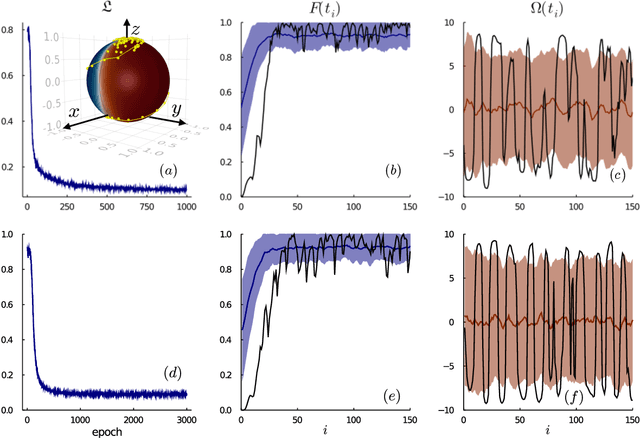
Controlling stochastic dynamics of a quantum system is an indispensable task in fields such as quantum information processing and metrology. Yet, there is no general ready-made approach to design efficient control strategies. Here, we propose a framework for the automated design of control schemes based on differentiable programming ($\partial \mathrm{P}$). We apply this approach to state preparation and stabilization of a qubit subjected to homodyne detection. To this end, we formulate the control task as an optimization problem where the loss function quantifies the distance from the target state and we employ neural networks (NNs) as controllers. The system's time evolution is governed by a stochastic differential equation (SDE). To implement efficient training, we backpropagate the gradient information from the loss function through the SDE solver using adjoint sensitivity methods. As a first example, we feed the quantum state to the controller and focus on different methods to obtain gradients. As a second example, we directly feed the homodyne detection signal to the controller. The instantaneous value of the homodyne current contains only very limited information on the actual state of the system, covered in unavoidable photon-number fluctuations. Despite the resulting poor signal-to-noise ratio, we can train our controller to prepare and stabilize the qubit to a target state with a mean fidelity around 85%. We also compare the solutions found by the NN to a hand-crafted control strategy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge