Automatic Double Reinforcement Learning in Semiparametric Markov Decision Processes with Applications to Long-Term Causal Inference

Double reinforcement learning (DRL) enables statistically efficient inference on the value of a policy in a nonparametric Markov Decision Process (MDP) given trajectories generated by another policy. However, this approach necessarily requires stringent overlap between the state distributions, which is often violated in practice. To relax this requirement and extend DRL, we study efficient inference on linear functionals of the $Q$-function (of which policy value is a special case) in infinite-horizon, time-invariant MDPs under semiparametric restrictions on the $Q$-function. These restrictions can reduce the overlap requirement and lower the efficiency bound, yielding more precise estimates. As an important example, we study the evaluation of long-term value under domain adaptation, given a few short trajectories from the new domain and restrictions on the difference between the domains. This can be used for long-term causal inference. Our method combines flexible estimates of the $Q$-function and the Riesz representer of the functional of interest (e.g., the stationary state density ratio for policy value) and is automatic in that we do not need to know the form of the latter - only the functional we care about. To address potential model misspecification bias, we extend the adaptive debiased machine learning (ADML) framework of \citet{van2023adaptive} to construct nonparametrically valid and superefficient estimators that adapt to the functional form of the $Q$-function. As a special case, we propose a novel adaptive debiased plug-in estimator that uses isotonic-calibrated fitted $Q$-iteration - a new calibration algorithm for MDPs - to circumvent the computational challenges of estimating debiasing nuisances from min-max objectives.

Beta Survival Models

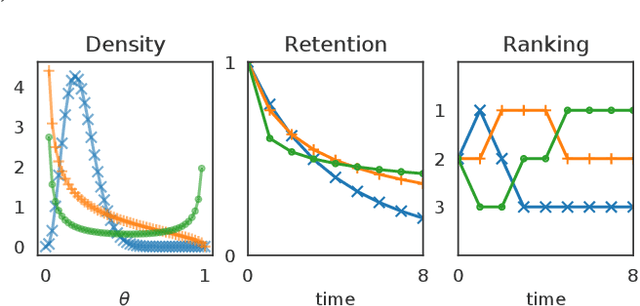
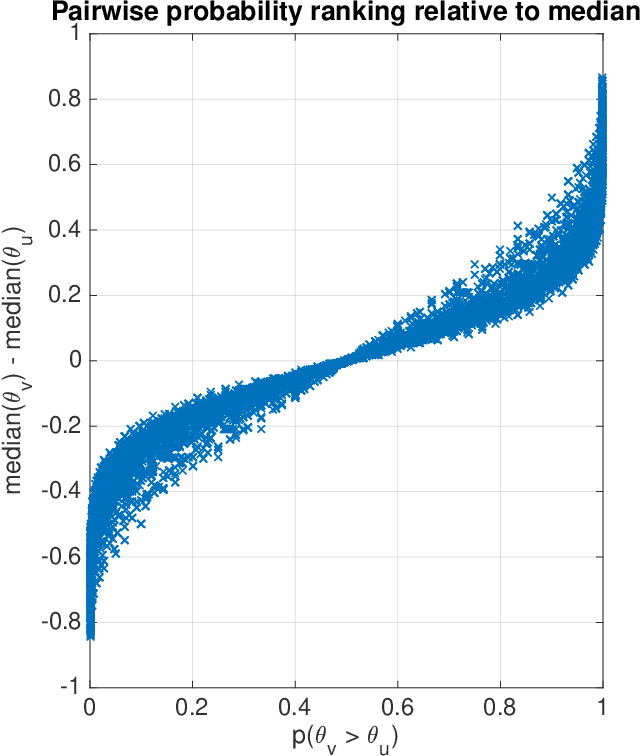
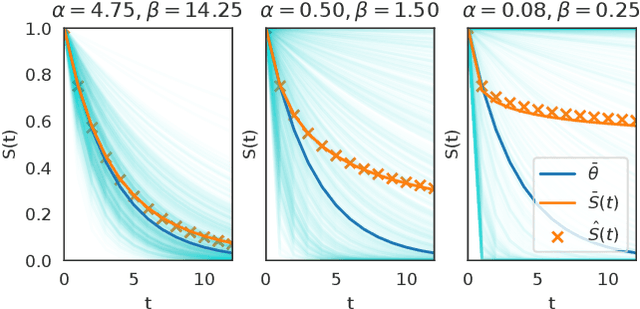
This article analyzes the problem of estimating the time until an event occurs, also known as survival modeling. We observe through substantial experiments on large real-world datasets and use-cases that populations are largely heterogeneous. Sub-populations have different mean and variance in their survival rates requiring flexible models that capture heterogeneity. We leverage a classical extension of the logistic function into the survival setting to characterize unobserved heterogeneity using the beta distribution. This yields insights into the geometry of the problem as well as efficient estimation methods for linear, tree and neural network models that adjust the beta distribution based on observed covariates. We also show that the additional information captured by the beta distribution leads to interesting ranking implications as we determine who is most-at-risk. We show theoretically that the ranking is variable as we forecast forward in time and prove that pairwise comparisons of survival remain transitive. Empirical results using large-scale datasets across two use-cases (online conversions and retention modeling), demonstrate the competitiveness of the method. The simplicity of the method and its ability to capture skew in the data makes it a viable alternative to standard techniques particularly when we are interested in the time to event and when the underlying probabilities are heterogeneous.