Beta Survival Models
Paper and Code
May 09, 2019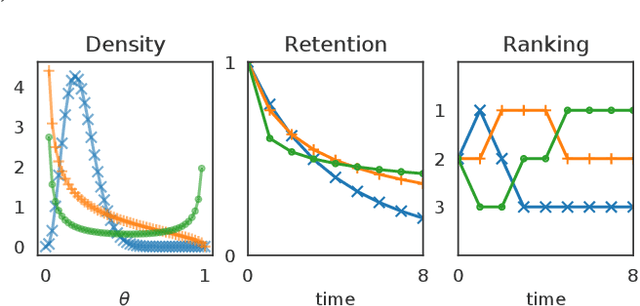

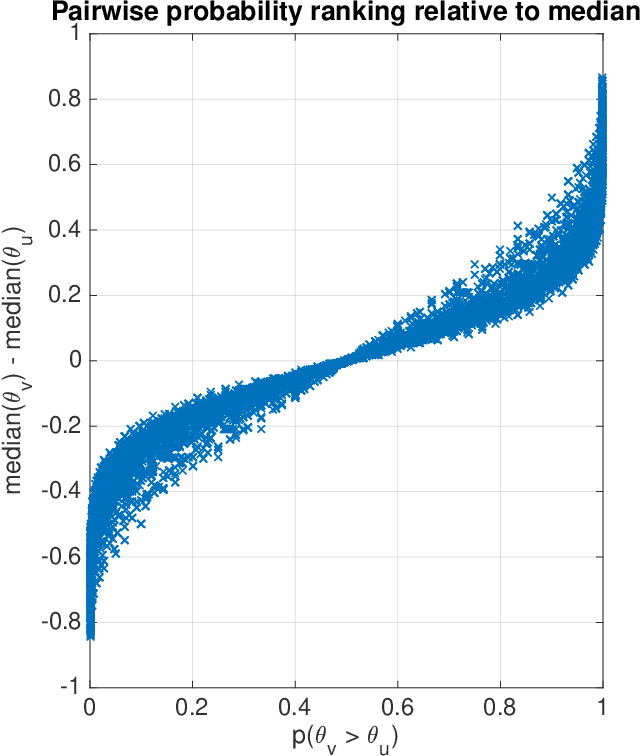
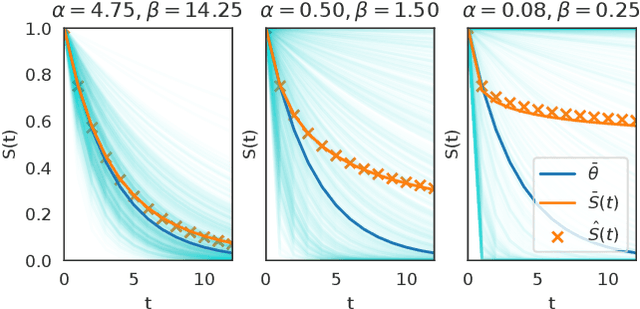
This article analyzes the problem of estimating the time until an event occurs, also known as survival modeling. We observe through substantial experiments on large real-world datasets and use-cases that populations are largely heterogeneous. Sub-populations have different mean and variance in their survival rates requiring flexible models that capture heterogeneity. We leverage a classical extension of the logistic function into the survival setting to characterize unobserved heterogeneity using the beta distribution. This yields insights into the geometry of the problem as well as efficient estimation methods for linear, tree and neural network models that adjust the beta distribution based on observed covariates. We also show that the additional information captured by the beta distribution leads to interesting ranking implications as we determine who is most-at-risk. We show theoretically that the ranking is variable as we forecast forward in time and prove that pairwise comparisons of survival remain transitive. Empirical results using large-scale datasets across two use-cases (online conversions and retention modeling), demonstrate the competitiveness of the method. The simplicity of the method and its ability to capture skew in the data makes it a viable alternative to standard techniques particularly when we are interested in the time to event and when the underlying probabilities are heterogeneous.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge