Collaborative targeted inference from continuously indexed nuisance parameter estimators
Paper and Code
Apr 05, 2018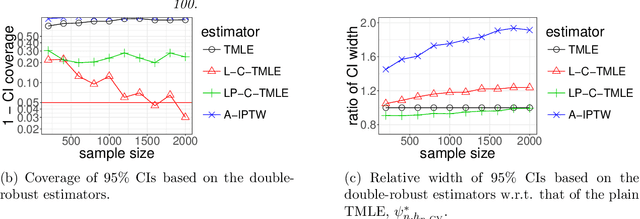
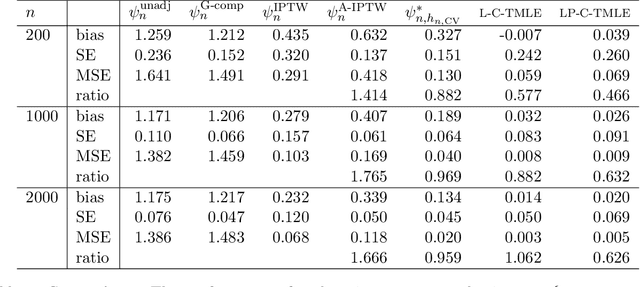
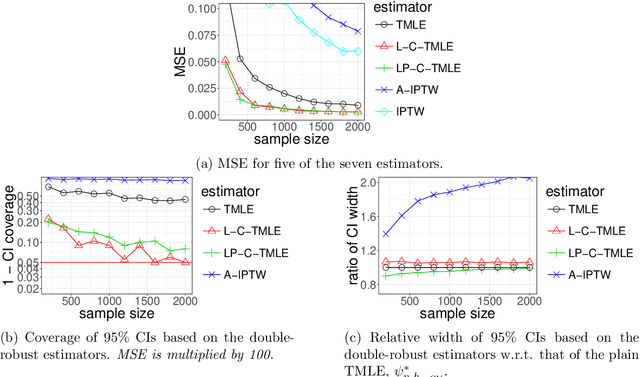
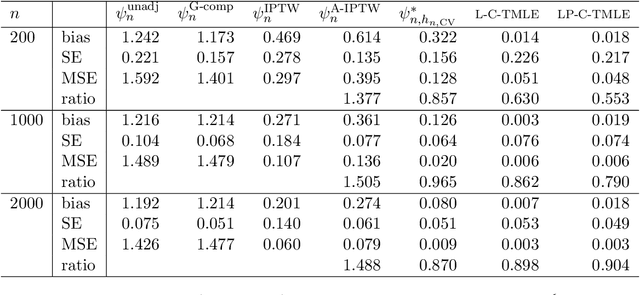
We wish to infer the value of a parameter at a law from which we sample independent observations. The parameter is smooth and we can define two variation-independent features of the law, its $Q$- and $G$-components, such that estimating them consistently at a fast enough product of rates allows to build a confidence interval (CI) with a given asymptotic level from a plain targeted minimum loss estimator (TMLE). Say that the above product is not fast enough and the algorithm for the $G$-component is fine-tuned by a real-valued $h$. A plain TMLE with an $h$ chosen by cross-validation would typically not yield a CI. We construct a collaborative TMLE (C-TMLE) and show under mild conditions that, if there exists an oracle $h$ that makes a bulky remainder term asymptotically Gaussian, then the C-TMLE yields a CI. We illustrate our findings with the inference of the average treatment effect. We conduct a simulation study where the $G$-component is estimated by the LASSO and $h$ is the bound on the coefficients' norms. It sheds light on small sample properties, in the face of low- to high-dimensional baseline covariates, and possibly positivity violation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge