Mixture of multilayer stochastic block models for multiview clustering

In this work, we propose an original method for aggregating multiple clustering coming from different sources of information. Each partition is encoded by a co-membership matrix between observations. Our approach uses a mixture of multilayer Stochastic Block Models (SBM) to group co-membership matrices with similar information into components and to partition observations into different clusters, taking into account their specificities within the components. The identifiability of the model parameters is established and a variational Bayesian EM algorithm is proposed for the estimation of these parameters. The Bayesian framework allows for selecting an optimal number of clusters and components. The proposed approach is compared using synthetic data with consensus clustering and tensor-based algorithms for community detection in large-scale complex networks. Finally, the method is utilized to analyze global food trading networks, leading to structures of interest.

Inference of Multiscale Gaussian Graphical Model

Gaussian Graphical Models (GGMs) are widely used for exploratory data analysis in various fields such as genomics, ecology, psychometry. In a high-dimensional setting, when the number of variables exceeds the number of observations by several orders of magnitude, the estimation of GGM is a difficult and unstable optimization problem. Clustering of variables or variable selection is often performed prior to GGM estimation. We propose a new method allowing to simultaneously infer a hierarchical clustering structure and the graphs describing the structure of independence at each level of the hierarchy. This method is based on solving a convex optimization problem combining a graphical lasso penalty with a fused type lasso penalty. Results on real and synthetic data are presented.

Sparsity by Worst-Case Penalties

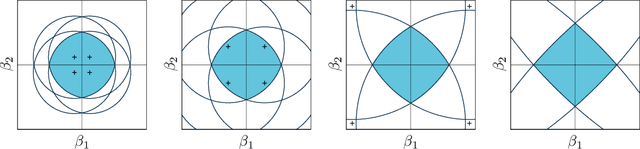
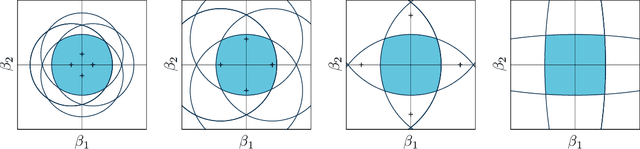
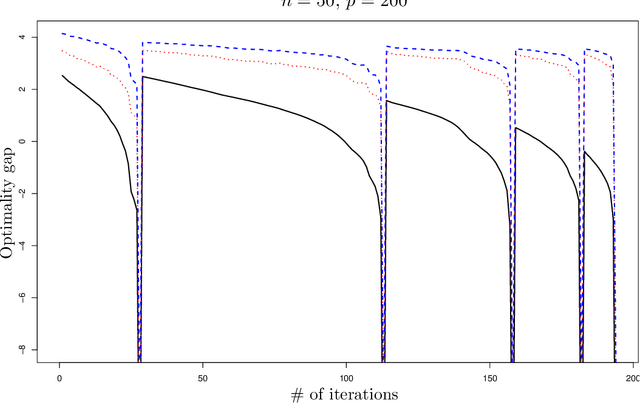
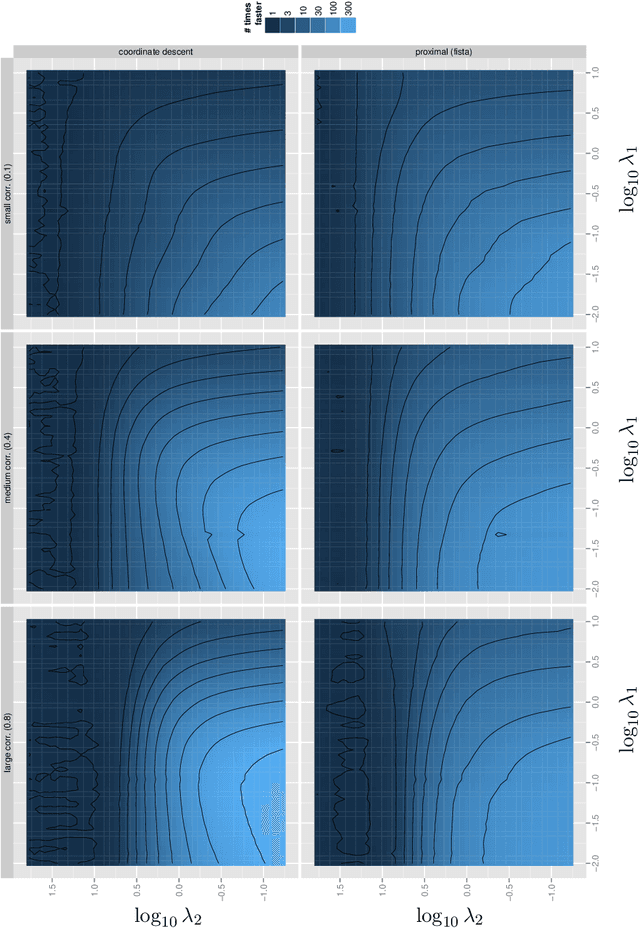
This paper proposes a new interpretation of sparse penalties such as the elastic-net and the group-lasso. Beyond providing a new viewpoint on these penalization schemes, our approach results in a unified optimization strategy. Our experiments demonstrate that this strategy, implemented on the elastic-net, is computationally extremely efficient for small to medium size problems. Our accompanying software solves problems very accurately, at machine precision, in the time required to get a rough estimate with competing state-of-the-art algorithms. We illustrate on real and artificial datasets that this accuracy is required to for the correctness of the support of the solution, which is an important element for the interpretability of sparsity-inducing penalties.

Strategies for online inference of model-based clustering in large and growing networks

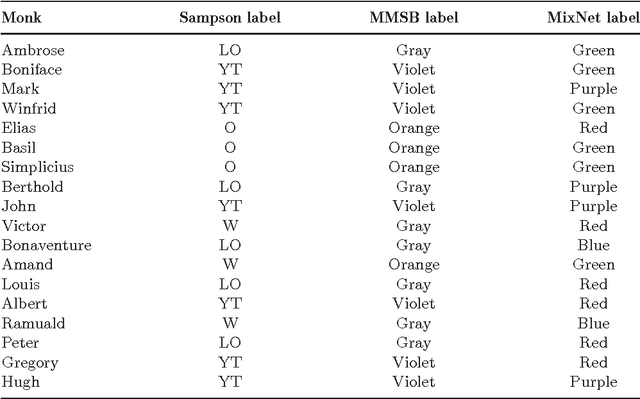
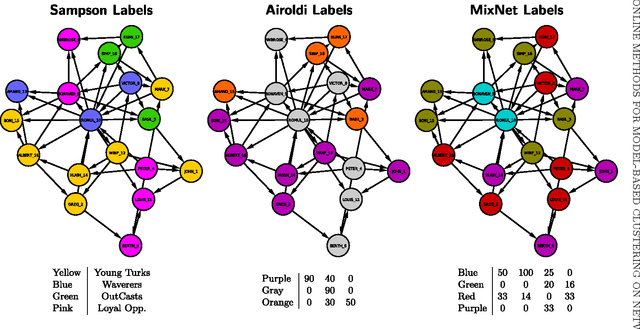
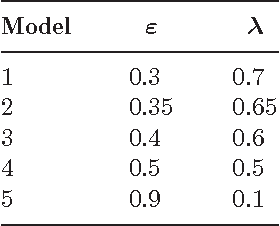
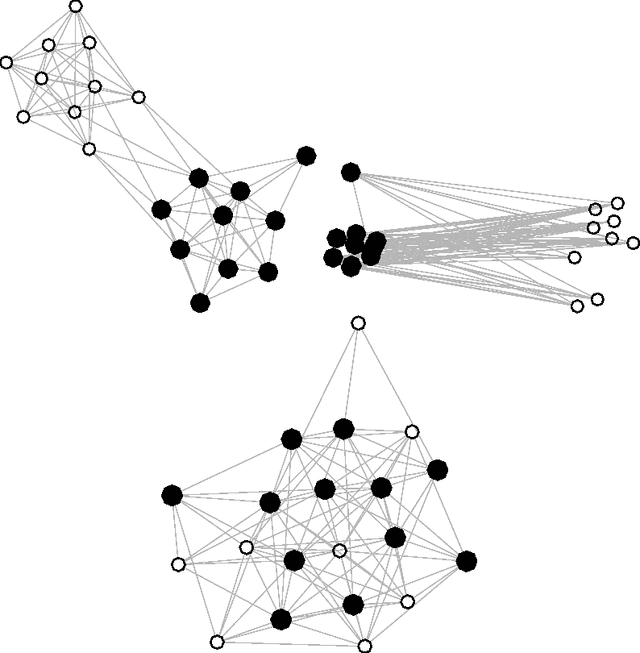
In this paper we adapt online estimation strategies to perform model-based clustering on large networks. Our work focuses on two algorithms, the first based on the SAEM algorithm, and the second on variational methods. These two strategies are compared with existing approaches on simulated and real data. We use the method to decipher the connexion structure of the political websphere during the US political campaign in 2008. We show that our online EM-based algorithms offer a good trade-off between precision and speed, when estimating parameters for mixture distributions in the context of random graphs.