PCA for Point Processes

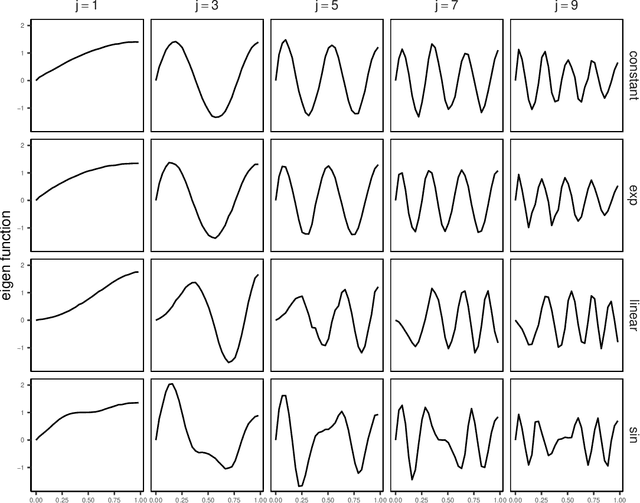
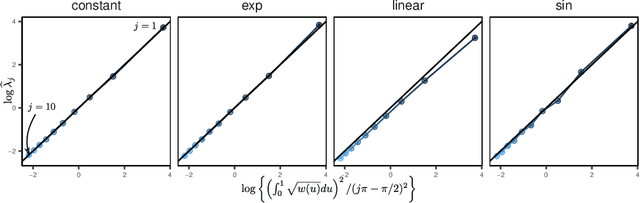
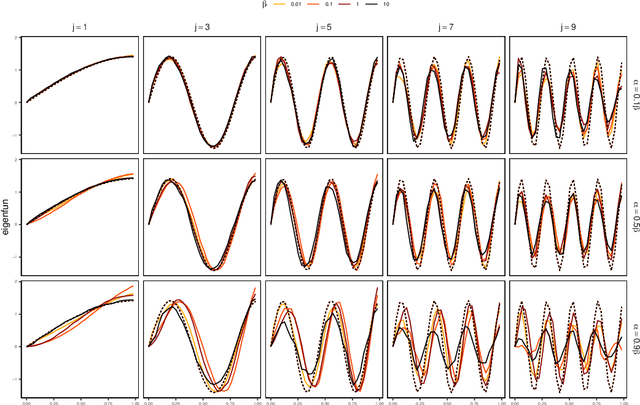
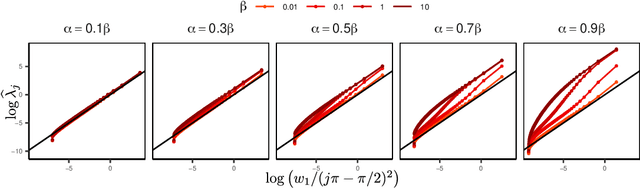
We introduce a novel statistical framework for the analysis of replicated point processes that allows for the study of point pattern variability at a population level. By treating point process realizations as random measures, we adopt a functional analysis perspective and propose a form of functional Principal Component Analysis (fPCA) for point processes. The originality of our method is to base our analysis on the cumulative mass functions of the random measures which gives us a direct and interpretable analysis. Key theoretical contributions include establishing a Karhunen-Lo\`{e}ve expansion for the random measures and a Mercer Theorem for covariance measures. We establish convergence in a strong sense, and introduce the concept of principal measures, which can be seen as latent processes governing the dynamics of the observed point patterns. We propose an easy-to-implement estimation strategy of eigenelements for which parametric rates are achieved. We fully characterize the solutions of our approach to Poisson and Hawkes processes and validate our methodology via simulations and diverse applications in seismology, single-cell biology and neurosiences, demonstrating its versatility and effectiveness. Our method is implemented in the pppca R-package.

Kernel-Based Testing for Single-Cell Differential Analysis

Single-cell technologies have provided valuable insights into the distribution of molecular features, such as gene expression and epigenomic modifications. However, comparing these complex distributions in a controlled and powerful manner poses methodological challenges. Here we propose to benefit from the kernel-testing framework to compare the complex cell-wise distributions of molecular features in a non-linear manner based on their kernel embedding. Our framework not only allows for feature-wise analyses but also enables global comparisons of transcriptomes or epigenomes, considering their intricate dependencies. By using a classifier to discriminate cells based on the variability of their embedding, our method uncovers heterogeneities in cell populations that would otherwise go undetected. We show that kernel testing overcomes the limitations of differential analysis methods dedicated to single-cell. Kernel testing is applied to investigate the reversion process of differentiating cells, successfully identifying cells in transition between reversion and differentiation stages. Additionally, we analyze single-cell ChIP-Seq data and identify a subpopulation of untreated breast cancer cells that exhibit an epigenomic profile similar to persister cells.

Strategies for online inference of model-based clustering in large and growing networks

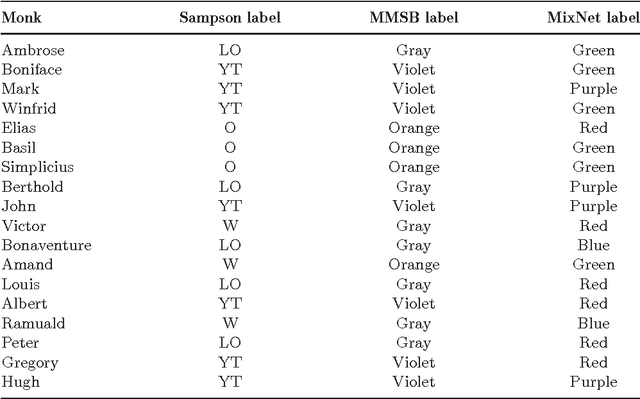
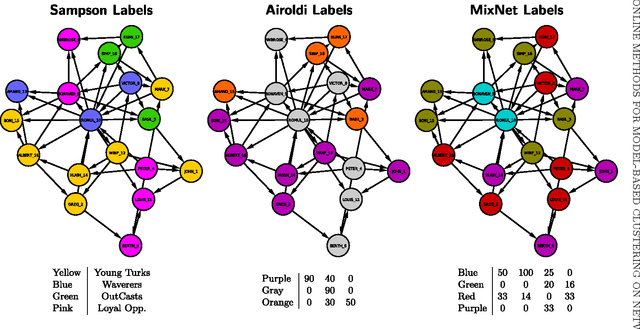
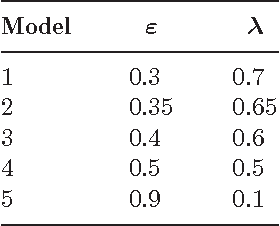
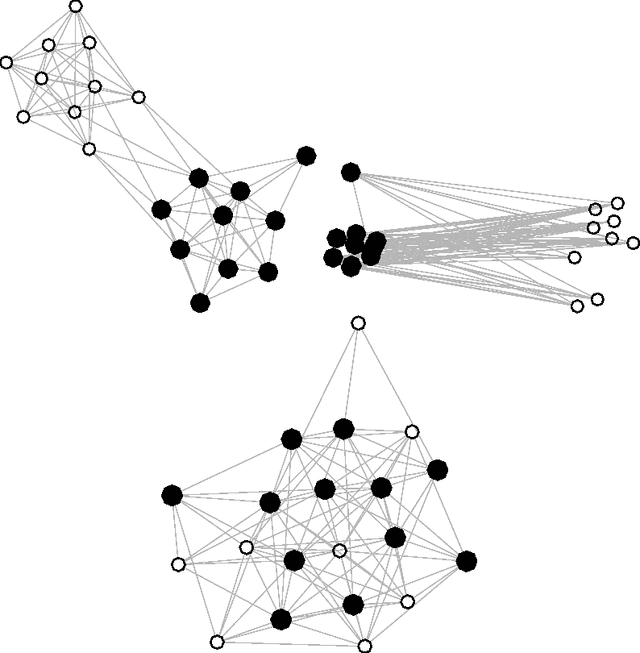
In this paper we adapt online estimation strategies to perform model-based clustering on large networks. Our work focuses on two algorithms, the first based on the SAEM algorithm, and the second on variational methods. These two strategies are compared with existing approaches on simulated and real data. We use the method to decipher the connexion structure of the political websphere during the US political campaign in 2008. We show that our online EM-based algorithms offer a good trade-off between precision and speed, when estimating parameters for mixture distributions in the context of random graphs.