UVIP: Model-Free Approach to Evaluate Reinforcement Learning Algorithms

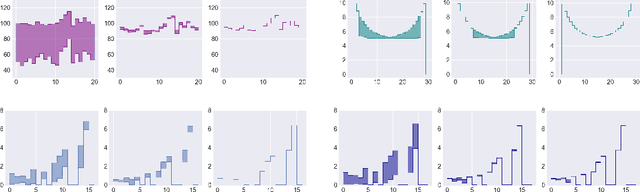
Policy evaluation is an important instrument for the comparison of different algorithms in Reinforcement Learning (RL). Yet even a precise knowledge of the value function $V^{\pi}$ corresponding to a policy $\pi$ does not provide reliable information on how far is the policy $\pi$ from the optimal one. We present a novel model-free upper value iteration procedure $({\sf UVIP})$ that allows us to estimate the suboptimality gap $V^{\star}(x) - V^{\pi}(x)$ from above and to construct confidence intervals for $V^\star$. Our approach relies on upper bounds to the solution of the Bellman optimality equation via martingale approach. We provide theoretical guarantees for ${\sf UVIP}$ under general assumptions and illustrate its performance on a number of benchmark RL problems.

Fast Incremental Expectation Maximization for finite-sum optimization: nonasymptotic convergence

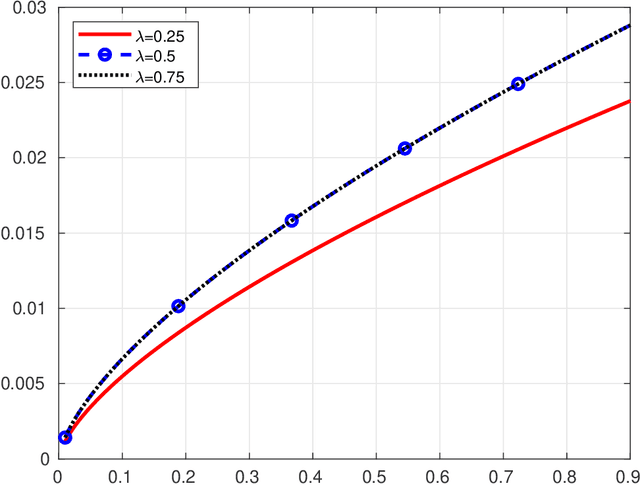
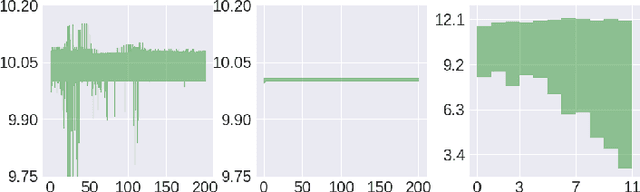
Fast Incremental Expectation Maximization (FIEM) is a version of the EM framework for large datasets. In this paper, we first recast FIEM and other incremental EM type algorithms in the {\em Stochastic Approximation within EM} framework. Then, we provide nonasymptotic bounds for the convergence in expectation as a function of the number of examples $n$ and of the maximal number of iterations $\kmax$. We propose two strategies for achieving an $\epsilon$-approximate stationary point, respectively with $\kmax = O(n^{2/3}/\epsilon)$ and $\kmax = O(\sqrt{n}/\epsilon^{3/2})$, both strategies relying on a random termination rule before $\kmax$ and on a constant step size in the Stochastic Approximation step. Our bounds provide some improvements on the literature. First, they allow $\kmax$ to scale as $\sqrt{n}$ which is better than $n^{2/3}$ which was the best rate obtained so far; it is at the cost of a larger dependence upon the tolerance $\epsilon$, thus making this control relevant for small to medium accuracy with respect to the number of examples $n$. Second, for the $n^{2/3}$-rate, the numerical illustrations show that thanks to an optimized choice of the step size and of the bounds in terms of quantities characterizing the optimization problem at hand, our results desig a less conservative choice of the step size and provide a better control of the convergence in expectation.

Variance reduction for Markov chains with application to MCMC

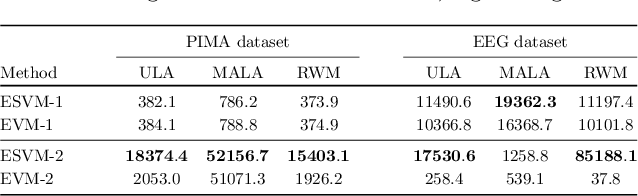
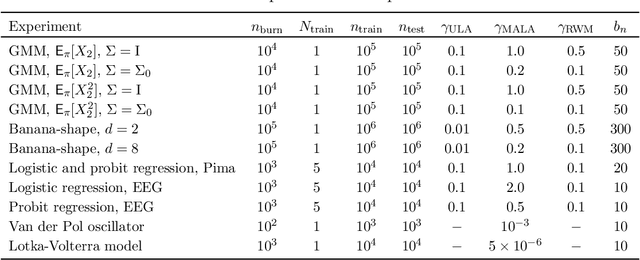
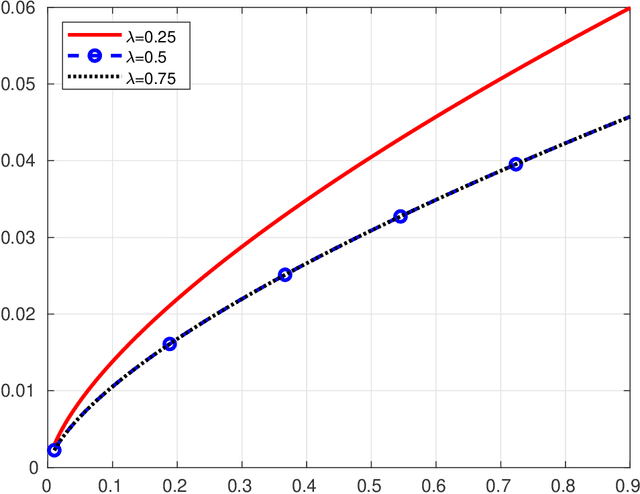
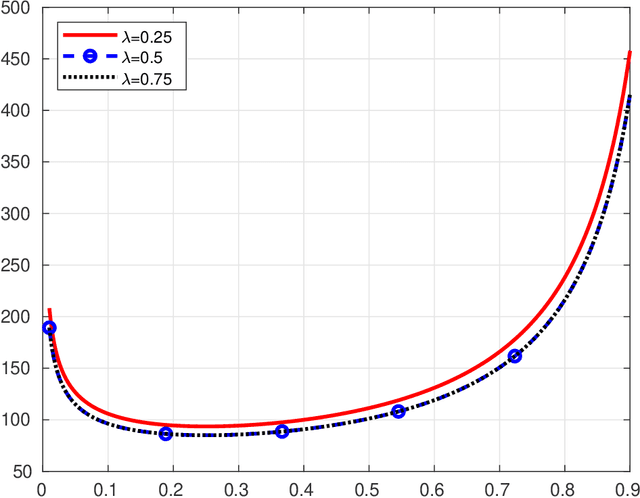
In this paper we propose a novel variance reduction approach for additive functionals of Markov chains based on minimization of an estimate for the asymptotic variance of these functionals over suitable classes of control variates. A distinctive feature of the proposed approach is its ability to significantly reduce the overall finite sample variance. This feature is theoretically demonstrated by means of a deep non asymptotic analysis of a variance reduced functional as well as by a thorough simulation study. In particular we apply our method to various MCMC Bayesian estimation problems where it favourably compares to the existing variance reduction approaches.

Variance reduction for MCMC methods via martingale representations

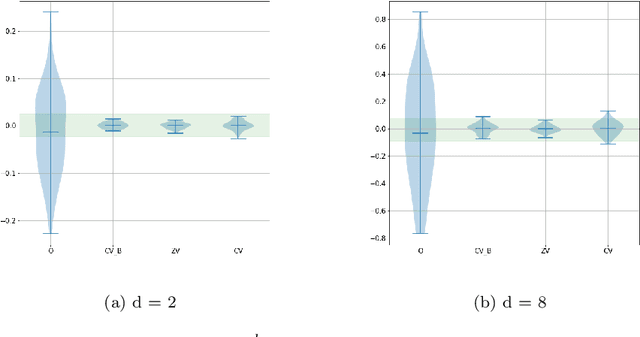
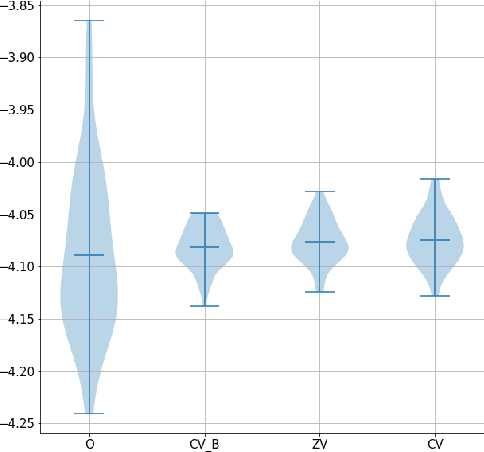
In this paper we propose an efficient variance reduction approach for MCMC algorithms relying on a novel discrete time martingale representation for Markov chains. Our approach is fully non-asymptotic and does not require any type of ergodicity or special product structure of the underlying density. By rigorously analyzing the convergence of the proposed algorithm, we show that it's complexity is indeed significantly smaller than one of the original MCMC algorithm. The numerical performance of the new method is illustrated in the case of Gaussian mixtures and binary regression.

Adaptive sequential Monte Carlo by means of mixture of experts

Appropriately designing the proposal kernel of particle filters is an issue of significant importance, since a bad choice may lead to deterioration of the particle sample and, consequently, waste of computational power. In this paper we introduce a novel algorithm adaptively approximating the so-called optimal proposal kernel by a mixture of integrated curved exponential distributions with logistic weights. This family of distributions, referred to as mixtures of experts, is broad enough to be used in the presence of multi-modality or strongly skewed distributions. The mixtures are fitted, via online-EM methods, to the optimal kernel through minimisation of the Kullback-Leibler divergence between the auxiliary target and instrumental distributions of the particle filter. At each iteration of the particle filter, the algorithm is required to solve only a single optimisation problem for the whole particle sample, yielding an algorithm with only linear complexity. In addition, we illustrate in a simulation study how the method can be successfully applied to optimal filtering in nonlinear state-space models.