UVIP: Model-Free Approach to Evaluate Reinforcement Learning Algorithms

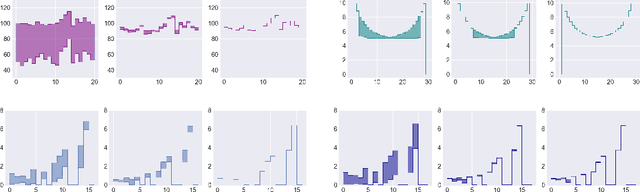
Policy evaluation is an important instrument for the comparison of different algorithms in Reinforcement Learning (RL). Yet even a precise knowledge of the value function $V^{\pi}$ corresponding to a policy $\pi$ does not provide reliable information on how far is the policy $\pi$ from the optimal one. We present a novel model-free upper value iteration procedure $({\sf UVIP})$ that allows us to estimate the suboptimality gap $V^{\star}(x) - V^{\pi}(x)$ from above and to construct confidence intervals for $V^\star$. Our approach relies on upper bounds to the solution of the Bellman optimality equation via martingale approach. We provide theoretical guarantees for ${\sf UVIP}$ under general assumptions and illustrate its performance on a number of benchmark RL problems.

Variance reduction for Markov chains with application to MCMC

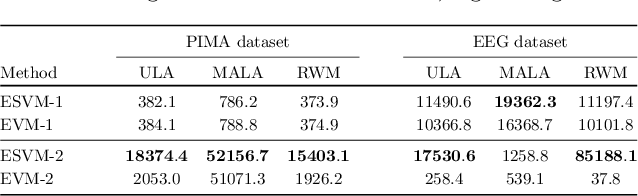
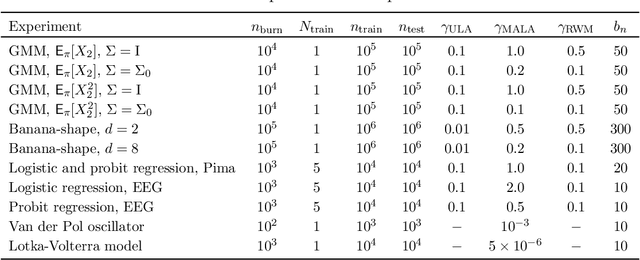
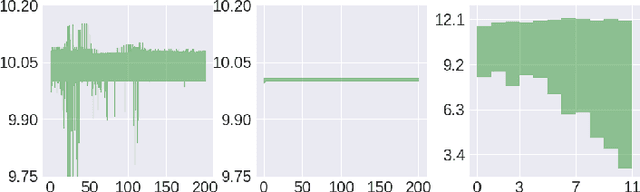
In this paper we propose a novel variance reduction approach for additive functionals of Markov chains based on minimization of an estimate for the asymptotic variance of these functionals over suitable classes of control variates. A distinctive feature of the proposed approach is its ability to significantly reduce the overall finite sample variance. This feature is theoretically demonstrated by means of a deep non asymptotic analysis of a variance reduced functional as well as by a thorough simulation study. In particular we apply our method to various MCMC Bayesian estimation problems where it favourably compares to the existing variance reduction approaches.