Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
M. Urusov
Variance reduction for MCMC methods via martingale representations
Mar 18, 2019Figures and Tables: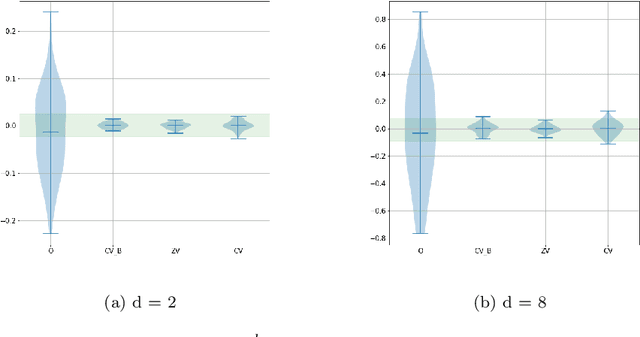
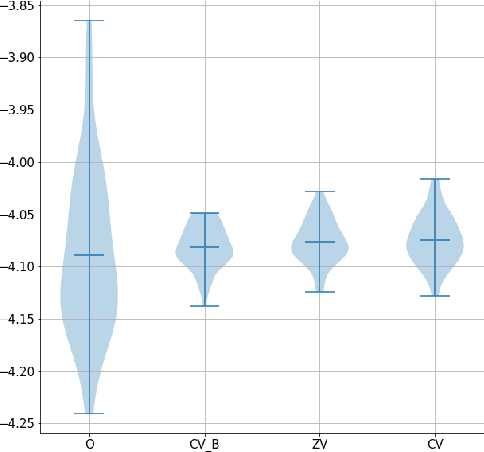

Abstract:In this paper we propose an efficient variance reduction approach for MCMC algorithms relying on a novel discrete time martingale representation for Markov chains. Our approach is fully non-asymptotic and does not require any type of ergodicity or special product structure of the underlying density. By rigorously analyzing the convergence of the proposed algorithm, we show that it's complexity is indeed significantly smaller than one of the original MCMC algorithm. The numerical performance of the new method is illustrated in the case of Gaussian mixtures and binary regression.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge