The Analytic Stockwell Transform and its Zeros

A recent original line of research in time--frequency analysis has shifted the interest in energy maxima toward zeros. Initially motivated by the intriguing uniform spread of the zeros of the spectrogram of white noise, it has led to fruitful theoretical developments combining probability theory, complex analysis and signal processing. In this vein, the present work proposes a characterization of the zeros of the Stockwell Transform of white noise, which consists in an hybrid time--frequency multiresolution representation. First of all, an analytic version of the Stockwell Transform is designed. Then, analyticity is leveraged to establish a connection with the hyperbolic Gaussian Analytic Function, whose zero set is invariant under the isometries of the Poincar\'e disk. Finally, the theoretical spatial statistics of the zeros of the hyperbolic Gaussian Analytic Function and the empirical statistics of the zeros the Analytic Stockwell Transform of white noise are compared through intensive Monte Carlo simulations, supporting the established connection. A publicly available documented Python toolbox accompanies this work.

Boosting the Sliding Frank-Wolfe solver for 3D deconvolution

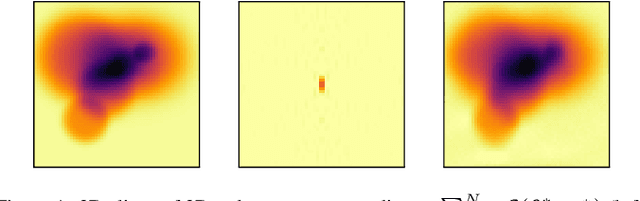
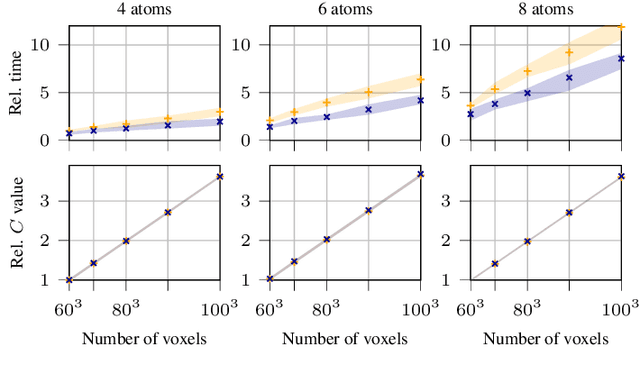
In the context of gridless sparse optimization, the Sliding Frank Wolfe algorithm recently introduced has shown interesting analytical and practical properties. Nevertheless, is application to large data, such as in the case of 3D deconvolution, is computationally heavy. In this paper, we investigate a strategy for leveraging this burden, in order to make this method more tractable for 3D deconvolution. We show that a boosted SFW can achieve the same results in a significantly reduced amount of time.