Anna Willmann
The Artificial Scientist -- in-transit Machine Learning of Plasma Simulations
Jan 06, 2025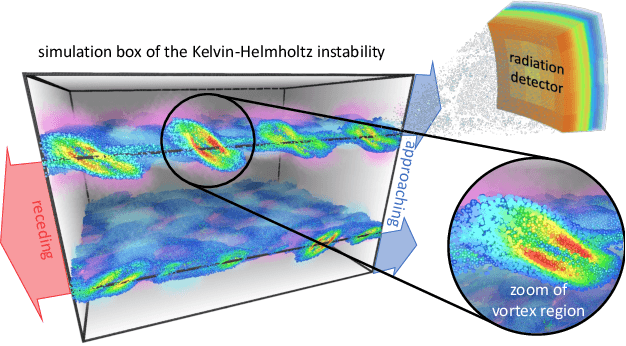
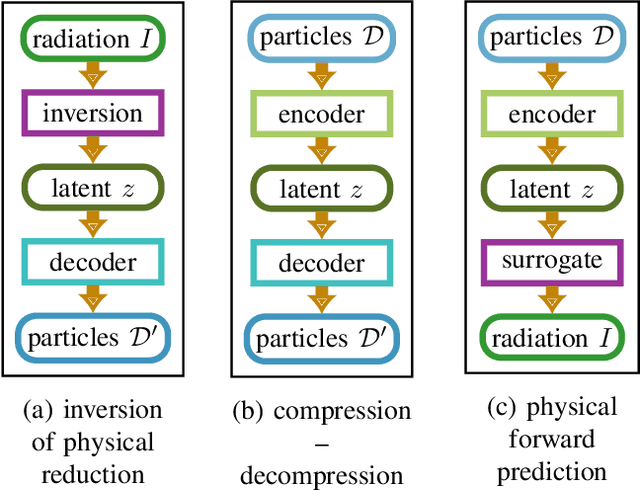
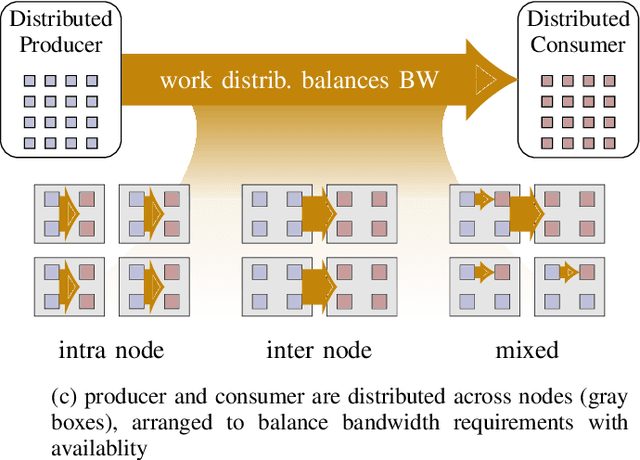
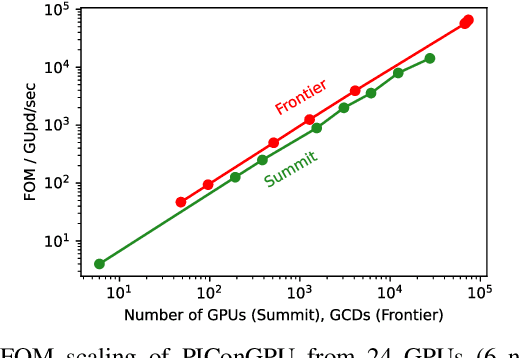
Abstract:Increasing HPC cluster sizes and large-scale simulations that produce petabytes of data per run, create massive IO and storage challenges for analysis. Deep learning-based techniques, in particular, make use of these amounts of domain data to extract patterns that help build scientific understanding. Here, we demonstrate a streaming workflow in which simulation data is streamed directly to a machine-learning (ML) framework, circumventing the file system bottleneck. Data is transformed in transit, asynchronously to the simulation and the training of the model. With the presented workflow, data operations can be performed in common and easy-to-use programming languages, freeing the application user from adapting the application output routines. As a proof-of-concept we consider a GPU accelerated particle-in-cell (PIConGPU) simulation of the Kelvin- Helmholtz instability (KHI). We employ experience replay to avoid catastrophic forgetting in learning from this non-steady process in a continual manner. We detail challenges addressed while porting and scaling to Frontier exascale system.
Ensuring Topological Data-Structure Preservation under Autoencoder Compression due to Latent Space Regularization in Gauss--Legendre nodes
Sep 21, 2023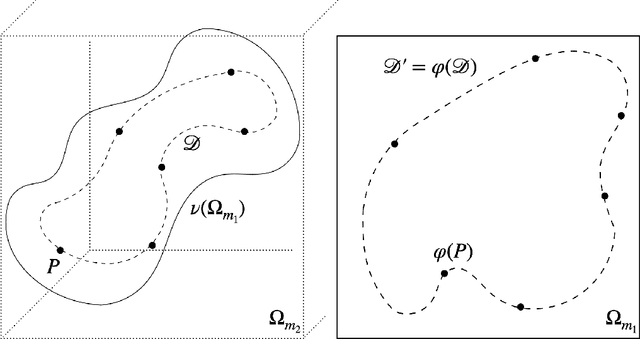
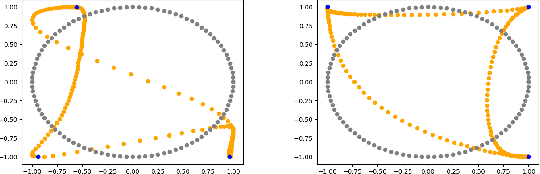
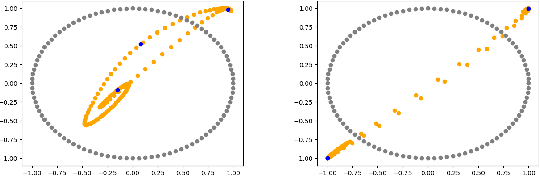
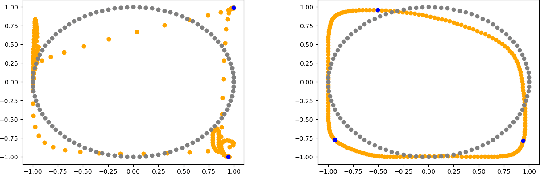
Abstract:We formulate a data independent latent space regularisation constraint for general unsupervised autoencoders. The regularisation rests on sampling the autoencoder Jacobian in Legendre nodes, being the centre of the Gauss-Legendre quadrature. Revisiting this classic enables to prove that regularised autoencoders ensure a one-to-one re-embedding of the initial data manifold to its latent representation. Demonstrations show that prior proposed regularisation strategies, such as contractive autoencoding, cause topological defects already for simple examples, and so do convolutional based (variational) autoencoders. In contrast, topological preservation is ensured already by standard multilayer perceptron neural networks when being regularised due to our contribution. This observation extends through the classic FashionMNIST dataset up to real world encoding problems for MRI brain scans, suggesting that, across disciplines, reliable low dimensional representations of complex high-dimensional datasets can be delivered due to this regularisation technique.
Learning Electron Bunch Distribution along a FEL Beamline by Normalising Flows
Feb 27, 2023Abstract:Understanding and control of Laser-driven Free Electron Lasers remain to be difficult problems that require highly intensive experimental and theoretical research. The gap between simulated and experimentally collected data might complicate studies and interpretation of obtained results. In this work we developed a deep learning based surrogate that could help to fill in this gap. We introduce a surrogate model based on normalising flows for conditional phase-space representation of electron clouds in a FEL beamline. Achieved results let us discuss further benefits and limitations in exploitability of the models to gain deeper understanding of fundamental processes within a beamline.
* 7 pages, 5 figures
Data-Driven Shadowgraph Simulation of a 3D Object
Jun 01, 2021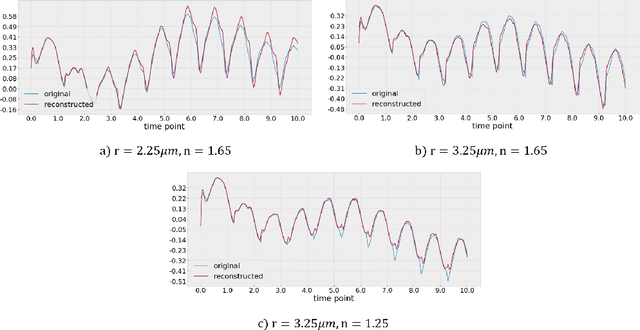
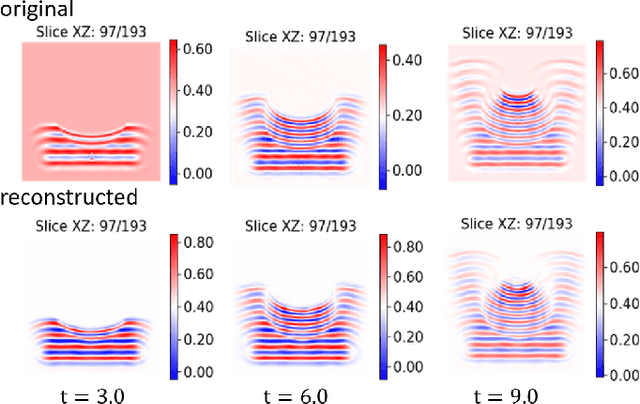
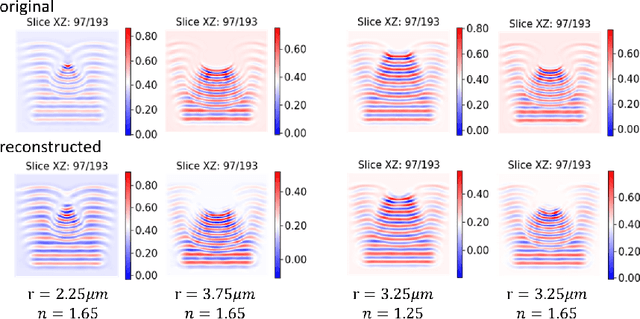
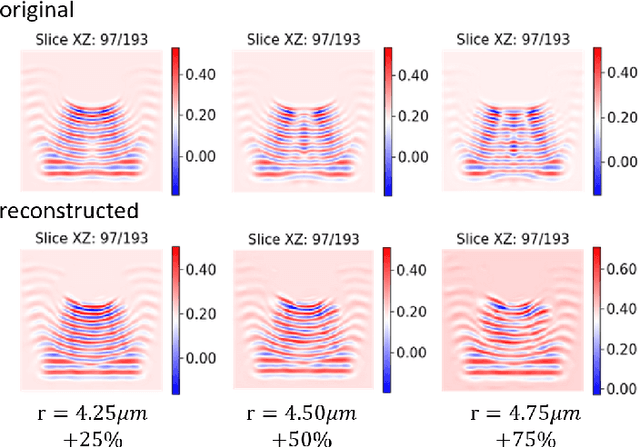
Abstract:In this work we propose a deep neural network based surrogate model for a plasma shadowgraph - a technique for visualization of perturbations in a transparent medium. We are substituting the numerical code by a computationally cheaper projection based surrogate model that is able to approximate the electric fields at a given time without computing all preceding electric fields as required by numerical methods. This means that the projection based surrogate model allows to recover the solution of the governing 3D partial differential equation, 3D wave equation, at any point of a given compute domain and configuration without the need to run a full simulation. This model has shown a good quality of reconstruction in a problem of interpolation of data within a narrow range of simulation parameters and can be used for input data of large size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge