Continual learning autoencoder training for a particle-in-cell simulation via streaming

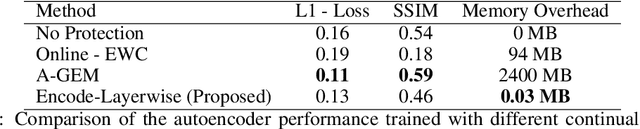
The upcoming exascale era will provide a new generation of physics simulations. These simulations will have a high spatiotemporal resolution, which will impact the training of machine learning models since storing a high amount of simulation data on disk is nearly impossible. Therefore, we need to rethink the training of machine learning models for simulations for the upcoming exascale era. This work presents an approach that trains a neural network concurrently to a running simulation without storing data on a disk. The training pipeline accesses the training data by in-memory streaming. Furthermore, we apply methods from the domain of continual learning to enhance the generalization of the model. We tested our pipeline on the training of a 3d autoencoder trained concurrently to laser wakefield acceleration particle-in-cell simulation. Furthermore, we experimented with various continual learning methods and their effect on the generalization.

Invertible Surrogate Models: Joint surrogate modelling and reconstruction of Laser-Wakefield Acceleration by invertible neural networks

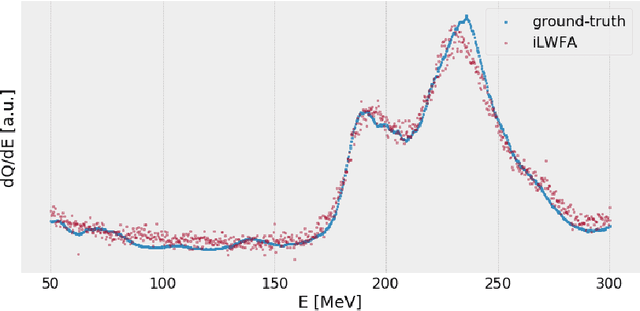
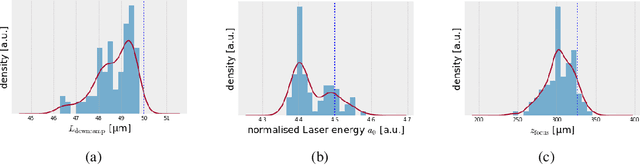
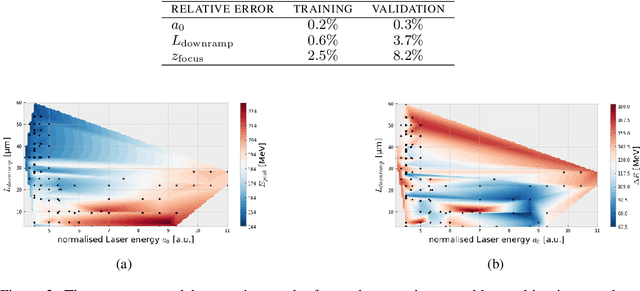
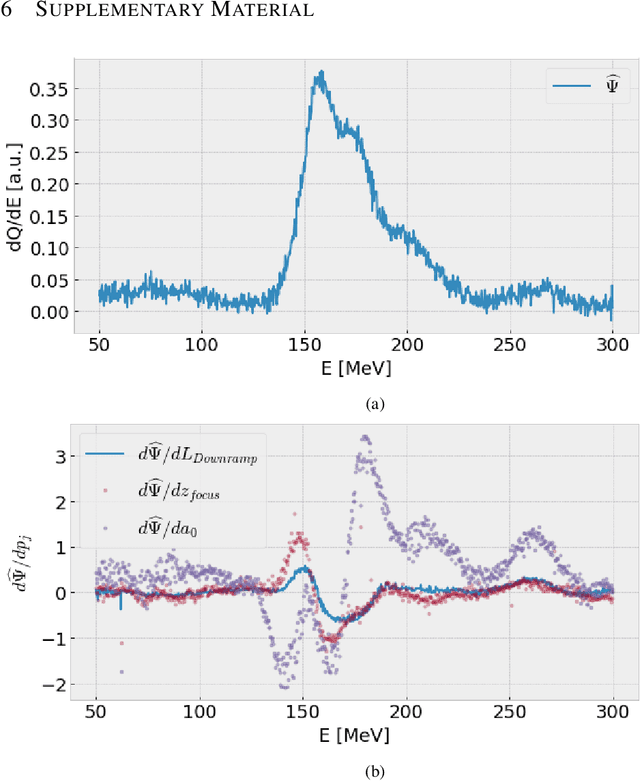
Invertible neural networks are a recent technique in machine learning promising neural network architectures that can be run in forward and reverse mode. In this paper, we will be introducing invertible surrogate models that approximate complex forward simulation of the physics involved in laser plasma accelerators: iLWFA. The bijective design of the surrogate model also provides all means for reconstruction of experimentally acquired diagnostics. The quality of our invertible laser wakefield acceleration network will be verified on a large set of numerical LWFA simulations.

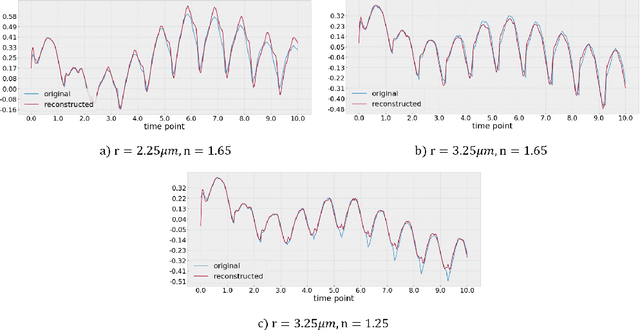
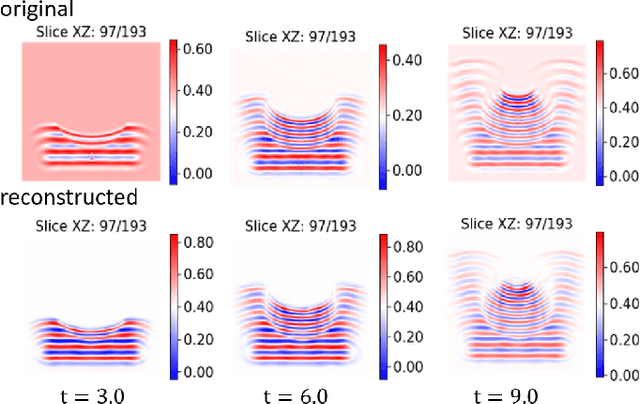
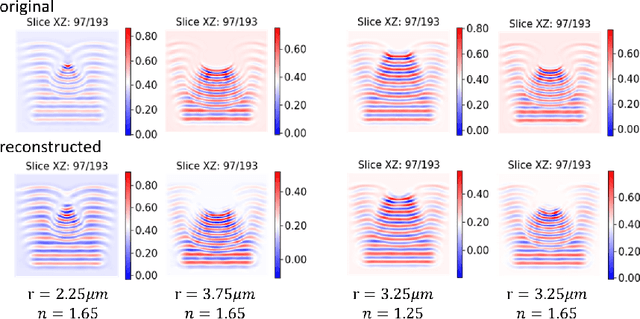
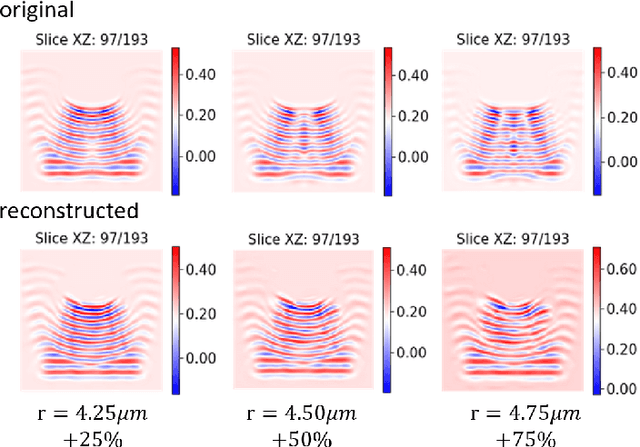
Data-Driven Shadowgraph Simulation of a 3D Object

In this work we propose a deep neural network based surrogate model for a plasma shadowgraph - a technique for visualization of perturbations in a transparent medium. We are substituting the numerical code by a computationally cheaper projection based surrogate model that is able to approximate the electric fields at a given time without computing all preceding electric fields as required by numerical methods. This means that the projection based surrogate model allows to recover the solution of the governing 3D partial differential equation, 3D wave equation, at any point of a given compute domain and configuration without the need to run a full simulation. This model has shown a good quality of reconstruction in a problem of interpolation of data within a narrow range of simulation parameters and can be used for input data of large size.

Large-scale Neural Solvers for Partial Differential Equations

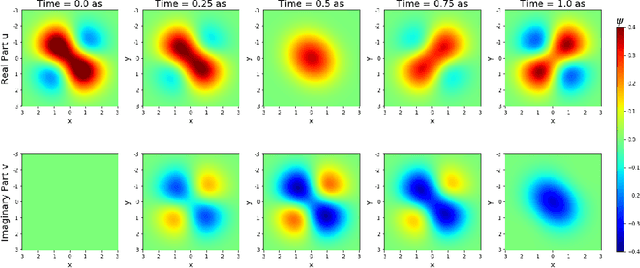
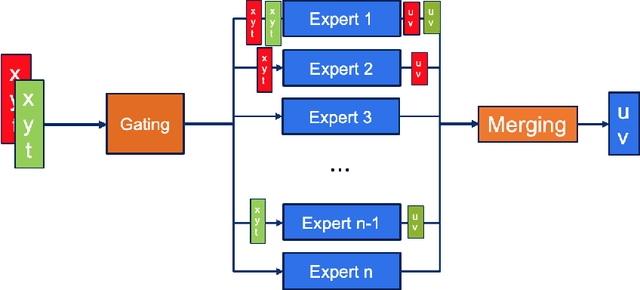
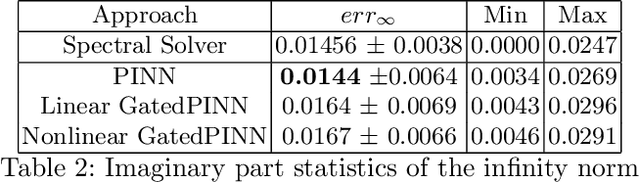
Solving partial differential equations (PDE) is an indispensable part of many branches of science as many processes can be modelled in terms of PDEs. However, recent numerical solvers require manual discretization of the underlying equation as well as sophisticated, tailored code for distributed computing. Scanning the parameters of the underlying model significantly increases the runtime as the simulations have to be cold-started for each parameter configuration. Machine Learning based surrogate models denote promising ways for learning complex relationship among input, parameter and solution. However, recent generative neural networks require lots of training data, i.e. full simulation runs making them costly. In contrast, we examine the applicability of continuous, mesh-free neural solvers for partial differential equations, physics-informed neural networks (PINNs) solely requiring initial/boundary values and validation points for training but no simulation data. The induced curse of dimensionality is approached by learning a domain decomposition that steers the number of neurons per unit volume and significantly improves runtime. Distributed training on large-scale cluster systems also promises great utilization of large quantities of GPUs which we assess by a comprehensive evaluation study. Finally, we discuss the accuracy of GatedPINN with respect to analytical solutions -- as well as state-of-the-art numerical solvers, such as spectral solvers.