Sunna Torge
Computational Performance Aware Benchmarking of Unsupervised Concept Drift Detection
Apr 17, 2023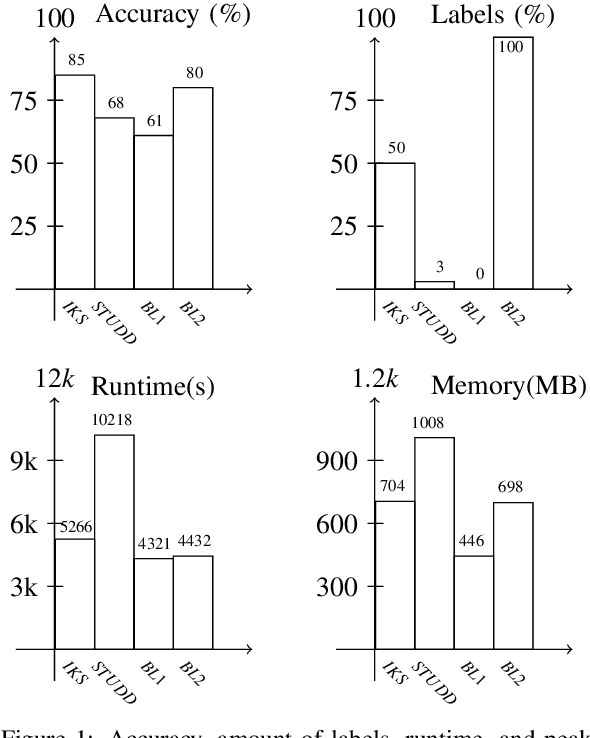
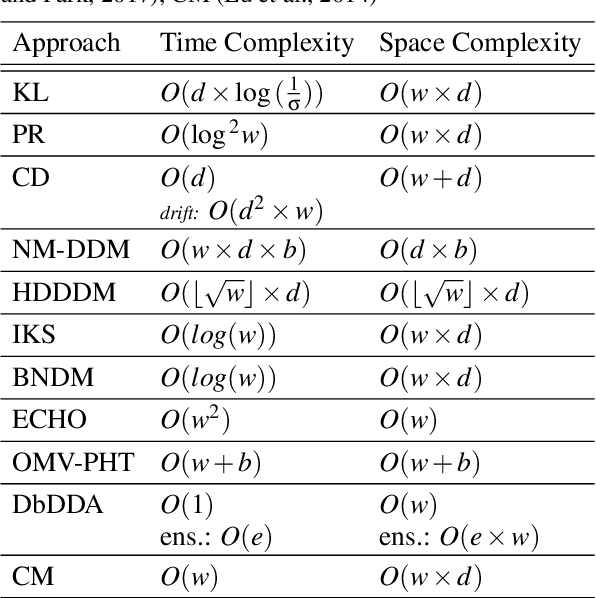
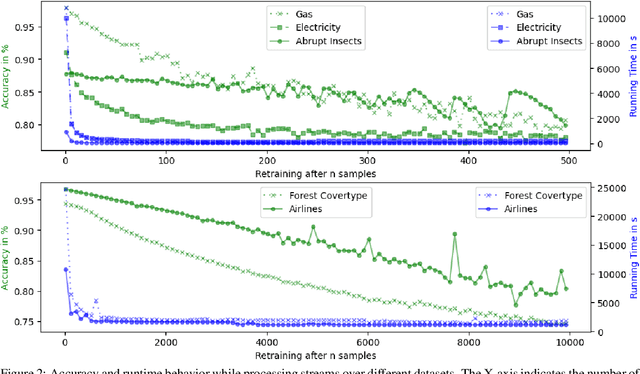
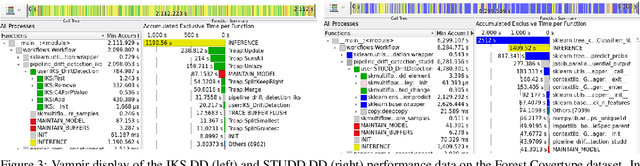
Abstract:For many AI systems, concept drift detection is crucial to ensure the systems reliability. These systems often have to deal with large amounts of data or react in real time. Thus, drift detectors must meet computational requirements or constraints with a comprehensive performance evaluation. However, so far, the focus of developing drift detectors is on detection quality, e.g.~accuracy, but not on computational performance, such as running time. We show that the previous works consider computational performance only as a secondary objective and do not have a benchmark for such evaluation. Hence, we propose a novel benchmark suite for drift detectors that accounts both detection quality and computational performance to ensure a detector's applicability in various AI systems. In this work, we focus on unsupervised drift detectors that are not restricted to the availability of labeled data and thus being widely applicable. Our benchmark suite supports configurable synthetic and real world data streams. Moreover, it provides means for simulating a machine learning model's output to unify the performance evaluation across different drift detectors. This allows a fair and comprehensive comparison of drift detectors proposed in related work. Our benchmark suite is integrated in the existing framework, Massive Online Analysis (MOA). To evaluate our benchmark suite's capability, we integrate two representative unsupervised drift detectors. Our work enables the scientific community to achieve a baseline for unsupervised drift detectors with respect to both detection quality and computational performance.
Large-scale Neural Solvers for Partial Differential Equations
Sep 08, 2020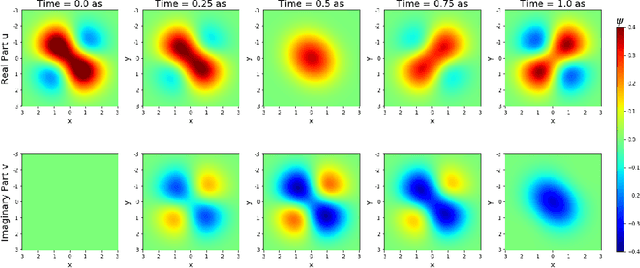

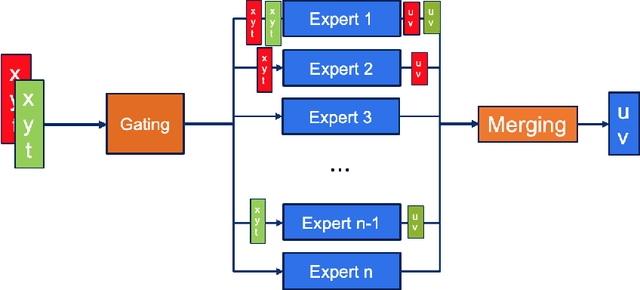
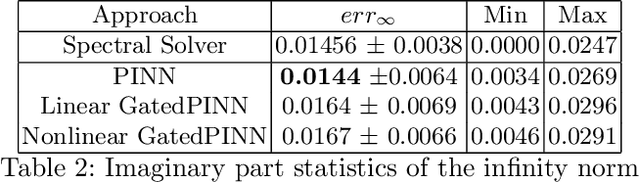
Abstract:Solving partial differential equations (PDE) is an indispensable part of many branches of science as many processes can be modelled in terms of PDEs. However, recent numerical solvers require manual discretization of the underlying equation as well as sophisticated, tailored code for distributed computing. Scanning the parameters of the underlying model significantly increases the runtime as the simulations have to be cold-started for each parameter configuration. Machine Learning based surrogate models denote promising ways for learning complex relationship among input, parameter and solution. However, recent generative neural networks require lots of training data, i.e. full simulation runs making them costly. In contrast, we examine the applicability of continuous, mesh-free neural solvers for partial differential equations, physics-informed neural networks (PINNs) solely requiring initial/boundary values and validation points for training but no simulation data. The induced curse of dimensionality is approached by learning a domain decomposition that steers the number of neurons per unit volume and significantly improves runtime. Distributed training on large-scale cluster systems also promises great utilization of large quantities of GPUs which we assess by a comprehensive evaluation study. Finally, we discuss the accuracy of GatedPINN with respect to analytical solutions -- as well as state-of-the-art numerical solvers, such as spectral solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge