Solving The Quantum Many-Body Hamiltonian Learning Problem with Neural Differential Equations

Understanding and characterising quantum many-body dynamics remains a significant challenge due to both the exponential complexity required to represent quantum many-body Hamiltonians, and the need to accurately track states in time under the action of such Hamiltonians. This inherent complexity limits our ability to characterise quantum many-body systems, highlighting the need for innovative approaches to unlock their full potential. To address this challenge, we propose a novel method to solve the Hamiltonian Learning (HL) problem-inferring quantum dynamics from many-body state trajectories-using Neural Differential Equations combined with an Ansatz Hamiltonian. Our method is reliably convergent, experimentally friendly, and interpretable, making it a stable solution for HL on a set of Hamiltonians previously unlearnable in the literature. In addition to this, we propose a new quantitative benchmark based on power laws, which can objectively compare the reliability and generalisation capabilities of any two HL algorithms. Finally, we benchmark our method against state-of-the-art HL algorithms with a 1D spin-1/2 chain proof of concept.

Efficient training of energy-based models via spin-glass control

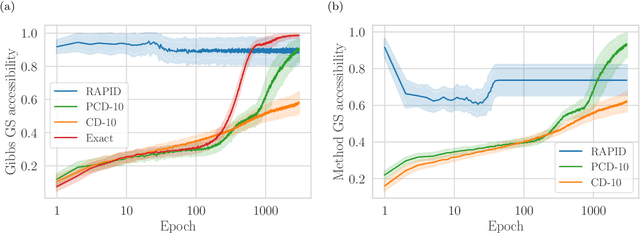
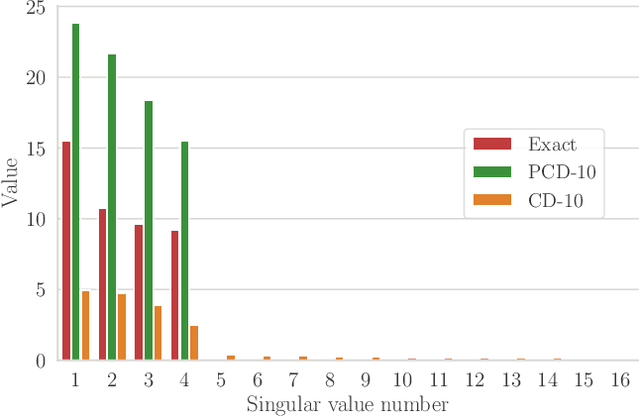
We present an efficient method for unsupervised learning using Boltzmann machines. The method is rooted in the control of the spin-glass properties of the Ising model described by the Boltzmann machine's weights. This allows for very easy access to low-energy configurations. We apply RAPID, the combination of Restricting the Axons (RA) of the model and training via Pattern-InDuced correlations (PID), to learn the Bars and Stripes dataset of various sizes and the MNIST dataset. We show how, in these tasks, RAPID quickly outperforms standard techniques for unsupervised learning in generalization ability. Indeed, both the number of epochs needed for effective learning and the computation time per training step are greatly reduced. In its simplest form, PID allows to compute the negative phase of the log-likelihood gradient with no Markov chain Monte Carlo sampling costs at all.

Quantum Inflation: A General Approach to Quantum Causal Compatibility

Causality is a seminal concept in science: any research discipline, from sociology and medicine to physics and chemistry, aims at understanding the causes that could explain the correlations observed among some measured variables. While several methods exist to characterize classical causal models, no general construction is known for the quantum case. In this work we present quantum inflation, a systematic technique to falsify if a given quantum causal model is compatible with some observed correlations. We demonstrate the power of the technique by reproducing known results and solving open problems for some paradigmatic examples of causal networks. Our results may find an application in many fields: from the characterization of correlations in quantum networks to the study of quantum effects in thermodynamic and biological processes.