Everything that can be learned about a causal structure with latent variables by observational and interventional probing schemes

What types of differences among causal structures with latent variables are impossible to distinguish by statistical data obtained by probing each visible variable? If the probing scheme is simply passive observation, then it is well-known that many different causal structures can realize the same joint probability distributions. Even for the simplest case of two visible variables, for instance, one cannot distinguish between one variable being a causal parent of the other and the two variables sharing a latent common cause. However, it is possible to distinguish between these two causal structures if we have recourse to more powerful probing schemes, such as the possibility of intervening on one of the variables and observing the other. Herein, we address the question of which causal structures remain indistinguishable even given the most informative types of probing schemes on the visible variables. We find that two causal structures remain indistinguishable if and only if they are both associated with the same mDAG structure (as defined by Evans (2016)). We also consider the question of when one causal structure dominates another in the sense that it can realize all of the joint probability distributions that can be realized by the other using a given probing scheme. (Equivalence of causal structures is the special case of mutual dominance.) Finally, we investigate to what extent one can weaken the probing schemes implemented on the visible variables and still have the same discrimination power as a maximally informative probing scheme.

Classifying Causal Structures: Ascertaining when Classical Correlations are Constrained by Inequalities

The classical causal relations between a set of variables, some observed and some latent, can induce both equality constraints (typically conditional independences) as well as inequality constraints (Instrumental and Bell inequalities being prototypical examples) on their compatible distribution over the observed variables. Enumerating a causal structure's implied inequality constraints is generally far more difficult than enumerating its equalities. Furthermore, only inequality constraints ever admit violation by quantum correlations. For both those reasons, it is important to classify causal scenarios into those which impose inequality constraints versus those which do not. Here we develop methods for detecting such scenarios by appealing to d-separation, e-separation, and incompatible supports. Many (perhaps all?) scenarios with exclusively equality constraints can be detected via a condition articulated by Henson, Lal and Pusey (HLP). Considering all scenarios with up to 4 observed variables, which number in the thousands, we are able to resolve all but three causal scenarios, providing evidence that the HLP condition is, in fact, exhaustive.

Entropic Inequality Constraints from $e$-separation Relations in Directed Acyclic Graphs with Hidden Variables

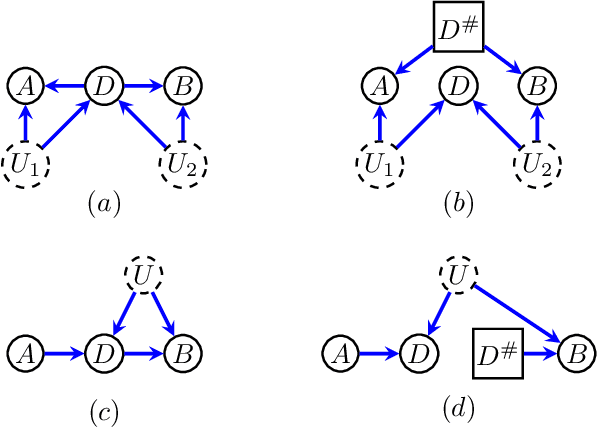
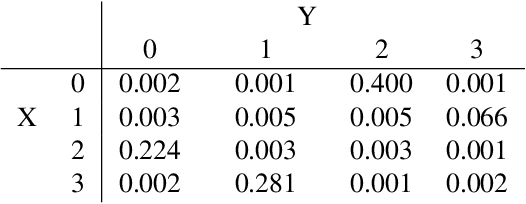
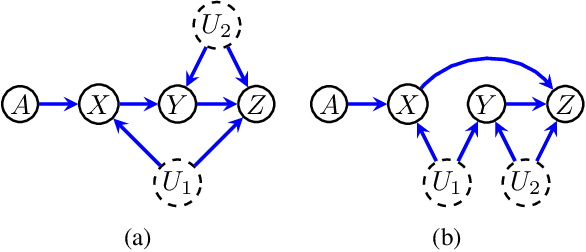
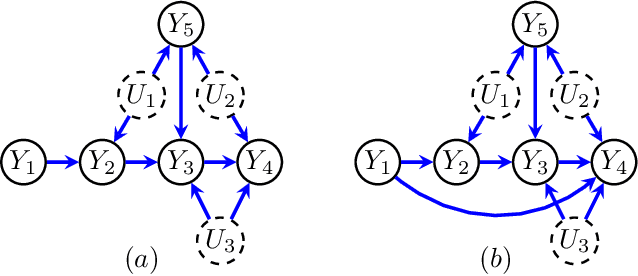
Directed acyclic graphs (DAGs) with hidden variables are often used to characterize causal relations between variables in a system. When some variables are unobserved, DAGs imply a notoriously complicated set of constraints on the distribution of observed variables. In this work, we present entropic inequality constraints that are implied by $e$-separation relations in hidden variable DAGs with discrete observed variables. The constraints can intuitively be understood to follow from the fact that the capacity of variables along a causal pathway to convey information is restricted by their entropy; e.g. at the extreme case, a variable with entropy $0$ can convey no information. We show how these constraints can be used to learn about the true causal model from an observed data distribution. In addition, we propose a measure of causal influence called the minimal mediary entropy, and demonstrate that it can augment traditional measures such as the average causal effect.

Causal networks and freedom of choice in Bell's theorem

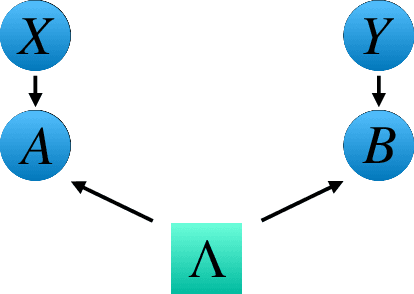
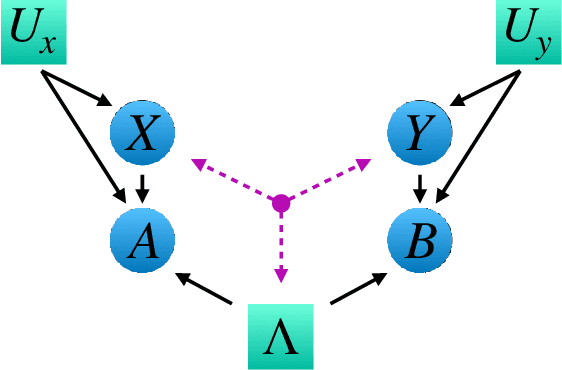
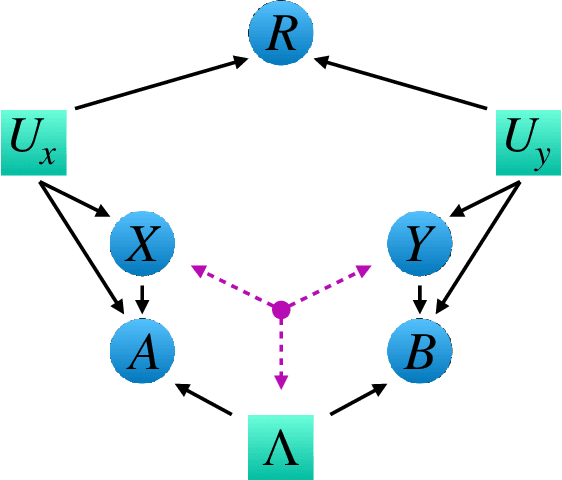
Bell's theorem is typically understood as the proof that quantum theory is incompatible with local hidden variable models. More generally, we can see the violation of a Bell inequality as witnessing the impossibility of explaining quantum correlations with classical causal models. The violation of a Bell inequality, however, does not exclude classical models where some level of measurement dependence is allowed, that is, the choice made by observers can be correlated with the source generating the systems to be measured. Here we show that the level of measurement dependence can be quantitatively upper bounded if we arrange the Bell test within a network. Furthermore, we also prove that these results can be adapted in order to derive non-linear Bell inequalities for a large class of causal networks and to identify quantumly realizable correlations which violate them.

Quantum Inflation: A General Approach to Quantum Causal Compatibility

Causality is a seminal concept in science: any research discipline, from sociology and medicine to physics and chemistry, aims at understanding the causes that could explain the correlations observed among some measured variables. While several methods exist to characterize classical causal models, no general construction is known for the quantum case. In this work we present quantum inflation, a systematic technique to falsify if a given quantum causal model is compatible with some observed correlations. We demonstrate the power of the technique by reproducing known results and solving open problems for some paradigmatic examples of causal networks. Our results may find an application in many fields: from the characterization of correlations in quantum networks to the study of quantum effects in thermodynamic and biological processes.

The Inflation Technique for Causal Inference with Latent Variables

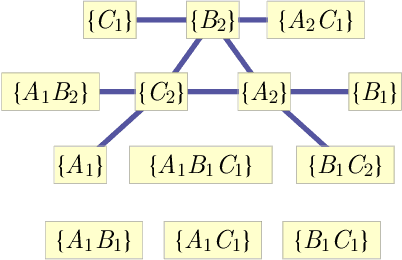
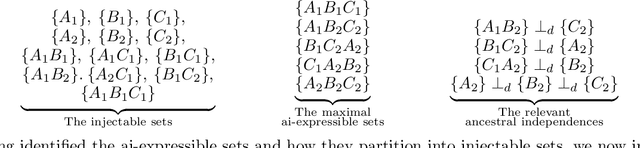
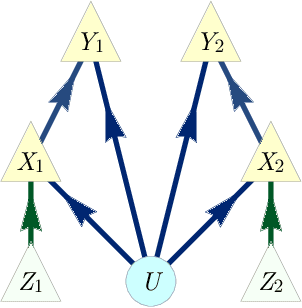
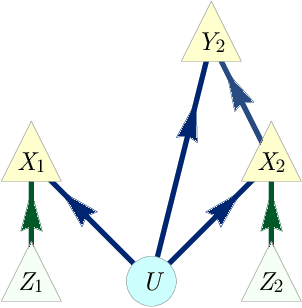
The problem of causal inference is to determine if a given probability distribution on observed variables is compatible with some causal structure. The difficult case is when the causal structure includes latent variables. We here introduce the $\textit{inflation technique}$ for tackling this problem. An inflation of a causal structure is a new causal structure that can contain multiple copies of each of the original variables, but where the ancestry of each copy mirrors that of the original. To every distribution of the observed variables that is compatible with the original causal structure, we assign a family of marginal distributions on certain subsets of the copies that are compatible with the inflated causal structure. It follows that compatibility constraints for the inflation can be translated into compatibility constraints for the original causal structure. Even if the constraints at the level of inflation are weak, such as observable statistical independences implied by disjoint causal ancestry, the translated constraints can be strong. We apply this method to derive new inequalities whose violation by a distribution witnesses that distribution's incompatibility with the causal structure (of which Bell inequalities and Pearl's instrumental inequality are prominent examples). We describe an algorithm for deriving all such inequalities for the original causal structure that follow from ancestral independences in the inflation. For three observed binary variables with pairwise common causes, it yields inequalities that are stronger in at least some aspects than those obtainable by existing methods. We also describe an algorithm that derives a weaker set of inequalities but is more efficient. Finally, we discuss which inflations are such that the inequalities one obtains from them remain valid even for quantum (and post-quantum) generalizations of the notion of a causal model.

The inflation technique solves completely the classical inference problem

The causal inference problem consists in determining whether a probability distribution over a set of observed variables is compatible with a given causal structure. In [arXiv:1609.00672], one of us introduced a hierarchy of necessary linear programming constraints which all the observed distributions compatible with the considered causal structure must satisfy. In this work, we prove that the inflation hierarchy is complete, i.e., any distribution of the observed variables which does not admit a realization within the considered causal structure will fail one of the inflation tests. More quantitatively, we show that any distribution of measurable events satisfying the $n^{th}$ inflation test is $O\left(\frac{1}{\sqrt{n}}\right)$-close in Euclidean norm to a distribution realizable within the given causal structure. In addition, we show that the corresponding $n^{th}$-order relaxation of the dual problem consisting in maximizing a $k^{th}$ degree polynomial on the observed variables is $O\left(\frac{k^2}{n}\right)$-close to the optimal solution.