Intensive Care as One Big Sequence Modeling Problem

Reinforcement Learning in Healthcare is typically concerned with narrow self-contained tasks such as sepsis prediction or anesthesia control. However, previous research has demonstrated the potential of generalist models (the prime example being Large Language Models) to outperform task-specific approaches due to their capability for implicit transfer learning. To enable training of foundation models for Healthcare as well as leverage the capabilities of state of the art Transformer architectures, we propose the paradigm of Healthcare as Sequence Modeling, in which interaction between the patient and the healthcare provider is represented as an event stream and tasks like diagnosis and treatment selection are modeled as prediction of future events in the stream. To explore this paradigm experimentally we develop MIMIC-SEQ, a sequence modeling benchmark derived by translating heterogenous clinical records from MIMIC-IV dataset into a uniform event stream format, train a baseline model and explore its capabilities.

The d-separation criterion in Categorical Probability

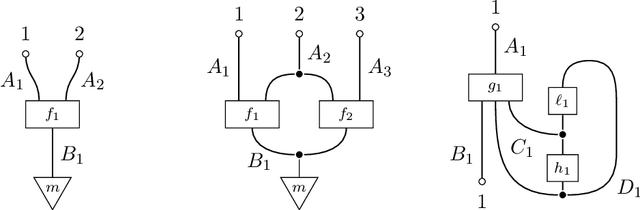
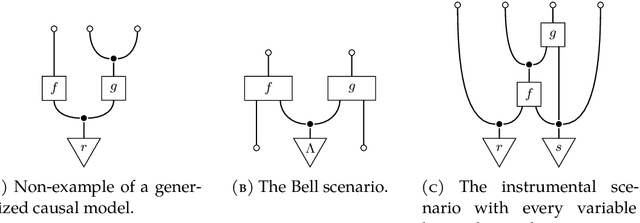
The d-separation criterion detects the compatibility of a joint probability distribution with a directed acyclic graph through certain conditional independences. In this work, we study this problem in the context of categorical probability theory by introducing a categorical definition of causal models, a categorical notion of d-separation, and proving an abstract version of the d-separation criterion. This approach has two main benefits. First, categorical d-separation is a very intuitive criterion based on topological connectedness. Second, our results apply in measure-theoretic probability (with standard Borel spaces), and therefore provide a clean proof of the equivalence of local and global Markov properties with causal compatibility for continuous and mixed variables.

The Inflation Technique for Causal Inference with Latent Variables

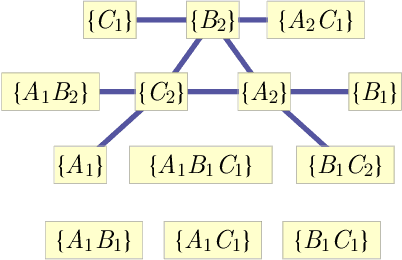
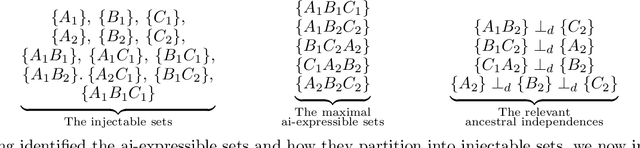
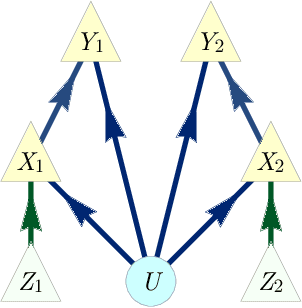
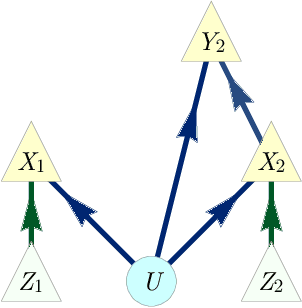
The problem of causal inference is to determine if a given probability distribution on observed variables is compatible with some causal structure. The difficult case is when the causal structure includes latent variables. We here introduce the $\textit{inflation technique}$ for tackling this problem. An inflation of a causal structure is a new causal structure that can contain multiple copies of each of the original variables, but where the ancestry of each copy mirrors that of the original. To every distribution of the observed variables that is compatible with the original causal structure, we assign a family of marginal distributions on certain subsets of the copies that are compatible with the inflated causal structure. It follows that compatibility constraints for the inflation can be translated into compatibility constraints for the original causal structure. Even if the constraints at the level of inflation are weak, such as observable statistical independences implied by disjoint causal ancestry, the translated constraints can be strong. We apply this method to derive new inequalities whose violation by a distribution witnesses that distribution's incompatibility with the causal structure (of which Bell inequalities and Pearl's instrumental inequality are prominent examples). We describe an algorithm for deriving all such inequalities for the original causal structure that follow from ancestral independences in the inflation. For three observed binary variables with pairwise common causes, it yields inequalities that are stronger in at least some aspects than those obtainable by existing methods. We also describe an algorithm that derives a weaker set of inequalities but is more efficient. Finally, we discuss which inflations are such that the inequalities one obtains from them remain valid even for quantum (and post-quantum) generalizations of the notion of a causal model.

Beyond Bell's Theorem II: Scenarios with arbitrary causal structure

It has recently been found that Bell scenarios are only a small subclass of interesting setups for studying the non-classical features of quantum theory within spacetime. We find that it is possible to talk about classical correlations, quantum correlations and other kinds of correlations on any directed acyclic graph, and this captures various extensions of Bell scenarios which have been considered in the literature. From a conceptual point of view, the main feature of our approach is its high level of unification: while the notions of source, choice of setting and measurement play all seemingly different roles in a Bell scenario, our formalism shows that they are all instances of the same concept of "event". Our work can also be understood as a contribution to the subject of causal inference with latent variables. Among other things, we introduce hidden Bayesian networks as a generalization of hidden Markov models.