Andreas Klingler
The d-separation criterion in Categorical Probability
Jul 12, 2022
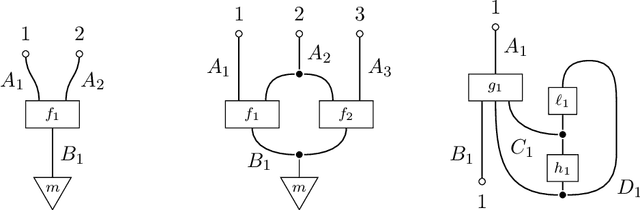
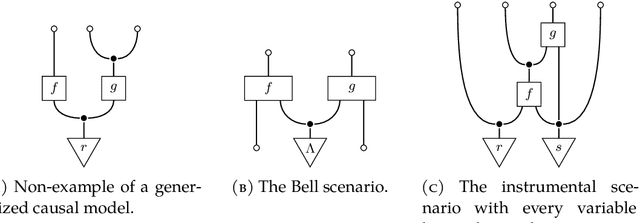
Abstract:The d-separation criterion detects the compatibility of a joint probability distribution with a directed acyclic graph through certain conditional independences. In this work, we study this problem in the context of categorical probability theory by introducing a categorical definition of causal models, a categorical notion of d-separation, and proving an abstract version of the d-separation criterion. This approach has two main benefits. First, categorical d-separation is a very intuitive criterion based on topological connectedness. Second, our results apply in measure-theoretic probability (with standard Borel spaces), and therefore provide a clean proof of the equivalence of local and global Markov properties with causal compatibility for continuous and mixed variables.
Cats climb entails mammals move: preserving hyponymy in compositional distributional semantics
May 29, 2020



Abstract:To give vector-based representations of meaning more structure, one approach is to use positive semidefinite (psd) matrices. These allow us to model similarity of words as well as the hyponymy or is-a relationship. Psd matrices can be learnt relatively easily in a given vector space $M\otimes M^*$, but to compose words to form phrases and sentences, we need representations in larger spaces. In this paper, we introduce a generic way of composing the psd matrices corresponding to words. We propose that psd matrices for verbs, adjectives, and other functional words be lifted to completely positive (CP) maps that match their grammatical type. This lifting is carried out by our composition rule called Compression, Compr. In contrast to previous composition rules like Fuzz and Phaser (a.k.a. KMult and BMult), Compr preserves hyponymy. Mathematically, Compr is itself a CP map, and is therefore linear and generally non-commutative. We give a number of proposals for the structure of Compr, based on spiders, cups and caps, and generate a range of composition rules. We test these rules on a small sentence entailment dataset, and see some improvements over the performance of Fuzz and Phaser.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge