Causal inference with imperfect instrumental variables

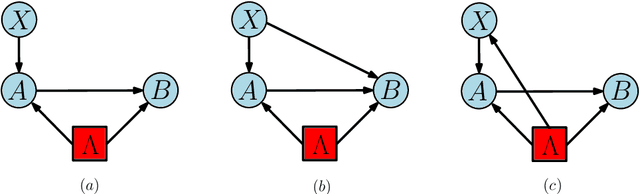
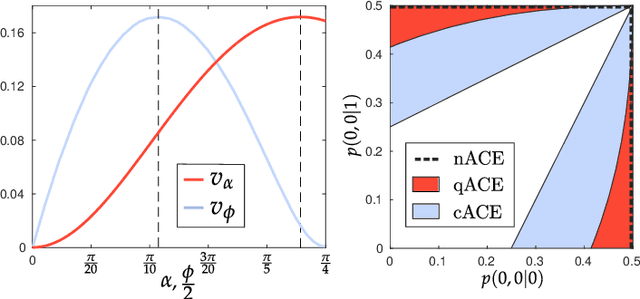
Instrumental variables allow for quantification of cause and effect relationships even in the absence of interventions. To achieve this, a number of causal assumptions must be met, the most important of which is the independence assumption, which states that the instrument and any confounding factor must be independent. However, if this independence condition is not met, can we still work with imperfect instrumental variables? Imperfect instruments can manifest themselves by violations of the instrumental inequalities that constrain the set of correlations in the scenario. In this paper, we establish a quantitative relationship between such violations of instrumental inequalities and the minimal amount of measurement dependence required to explain them. As a result, we provide adapted inequalities that are valid in the presence of a relaxed measurement dependence assumption in the instrumental scenario. This allows for the adaptation of existing and new lower bounds on the average causal effect for instrumental scenarios with binary outcomes. Finally, we discuss our findings in the context of quantum mechanics.

Ab-initio experimental violation of Bell inequalities

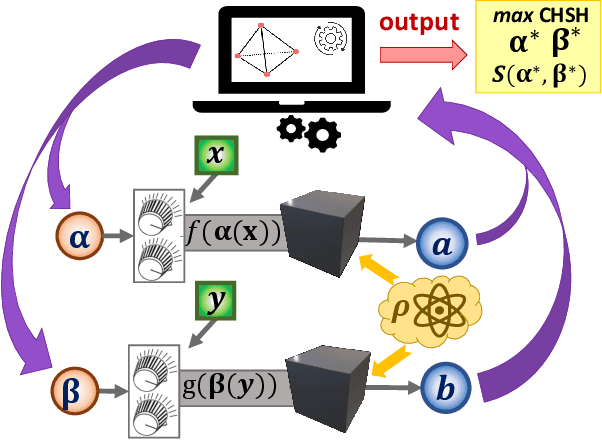
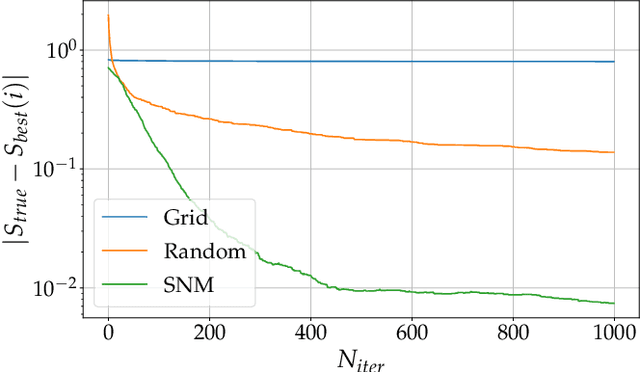
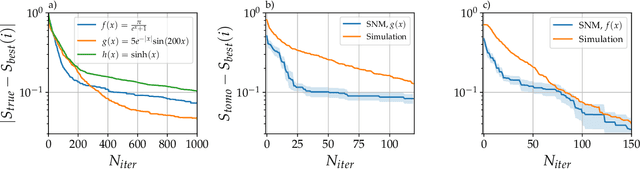
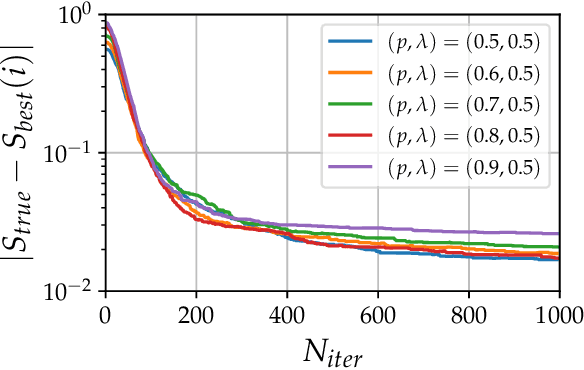
The violation of a Bell inequality is the paradigmatic example of device-independent quantum information: the nonclassicality of the data is certified without the knowledge of the functioning of devices. In practice, however, all Bell experiments rely on the precise understanding of the underlying physical mechanisms. Given that, it is natural to ask: Can one witness nonclassical behaviour in a truly black-box scenario? Here we propose and implement, computationally and experimentally, a solution to this ab-initio task. It exploits a robust automated optimization approach based on the Stochastic Nelder-Mead algorithm. Treating preparation and measurement devices as black-boxes, and relying on the observed statistics only, our adaptive protocol approaches the optimal Bell inequality violation after a limited number of iterations for a variety photonic states, measurement responses and Bell scenarios. In particular, we exploit it for randomness certification from unknown states and measurements. Our results demonstrate the power of automated algorithms, opening a new venue for the experimental implementation of device-independent quantum technologies.

Causal networks and freedom of choice in Bell's theorem

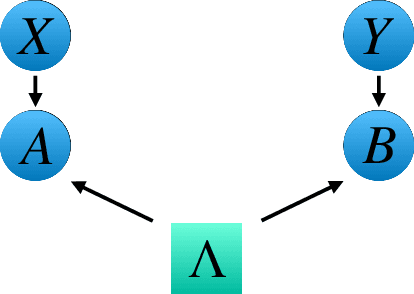
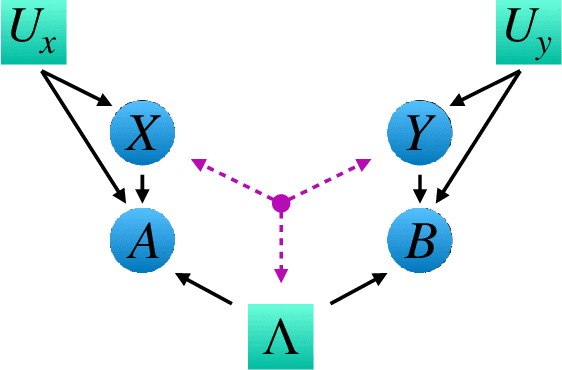
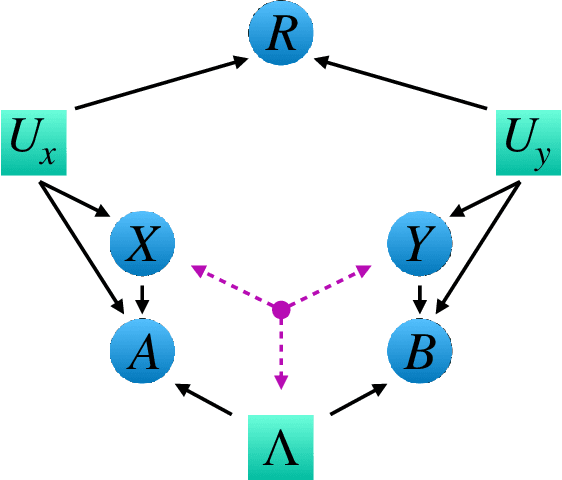
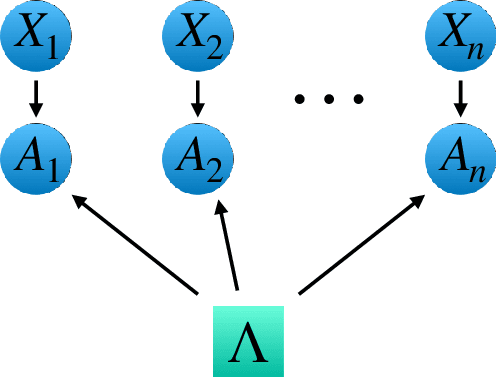
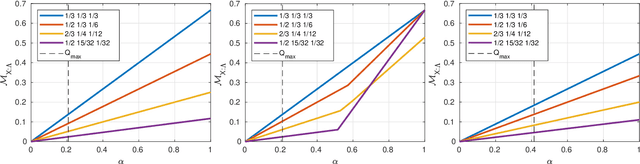
Bell's theorem is typically understood as the proof that quantum theory is incompatible with local hidden variable models. More generally, we can see the violation of a Bell inequality as witnessing the impossibility of explaining quantum correlations with classical causal models. The violation of a Bell inequality, however, does not exclude classical models where some level of measurement dependence is allowed, that is, the choice made by observers can be correlated with the source generating the systems to be measured. Here we show that the level of measurement dependence can be quantitatively upper bounded if we arrange the Bell test within a network. Furthermore, we also prove that these results can be adapted in order to derive non-linear Bell inequalities for a large class of causal networks and to identify quantumly realizable correlations which violate them.

Quantifying causal influences in the presence of a quantum common cause

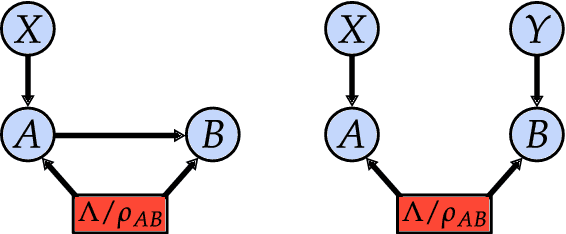
Quantum mechanics challenges our intuition on the cause-effect relations in nature. Some fundamental concepts, including Reichenbach's common cause principle or the notion of local realism, have to be reconsidered. Traditionally, this is witnessed by the violation of a Bell inequality. But are Bell inequalities the only signature of the incompatibility between quantum correlations and causality theory? Motivated by this question we introduce a general framework able to estimate causal influences between two variables, without the need of interventions and irrespectively of the classical, quantum, or even post-quantum nature of a common cause. In particular, by considering the simplest instrumental scenario -- for which violation of Bell inequalities is not possible -- we show that every pure bipartite entangled state violates the classical bounds on causal influence, thus answering in negative to the posed question and opening a new venue to explore the role of causality within quantum theory.

Unveiling phase transitions with machine learning

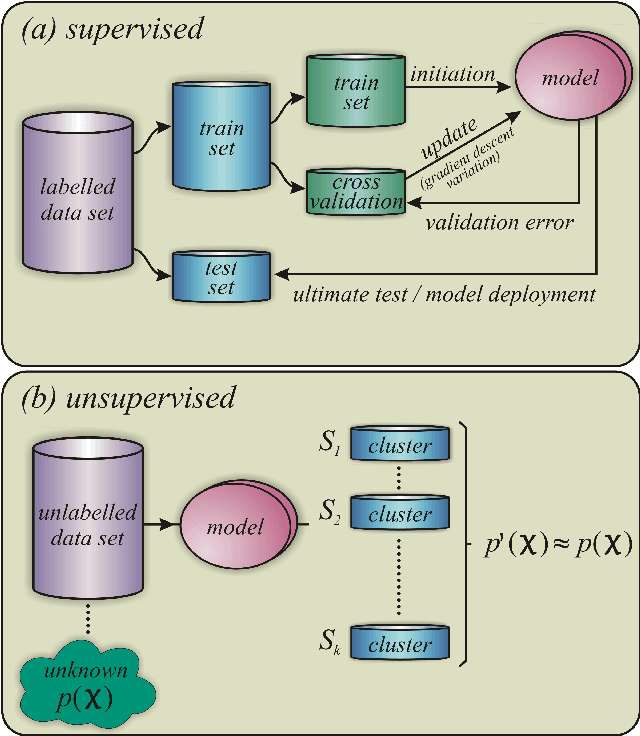
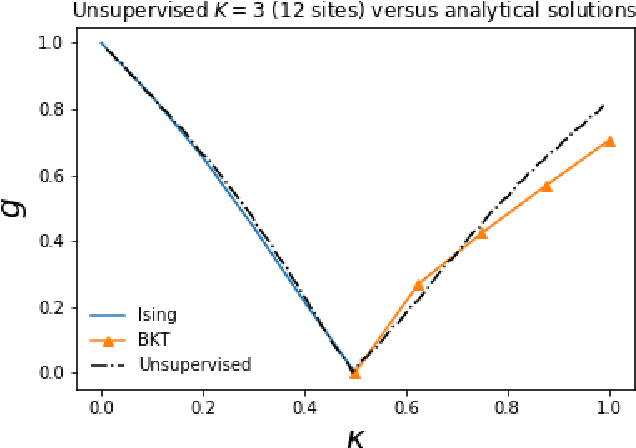
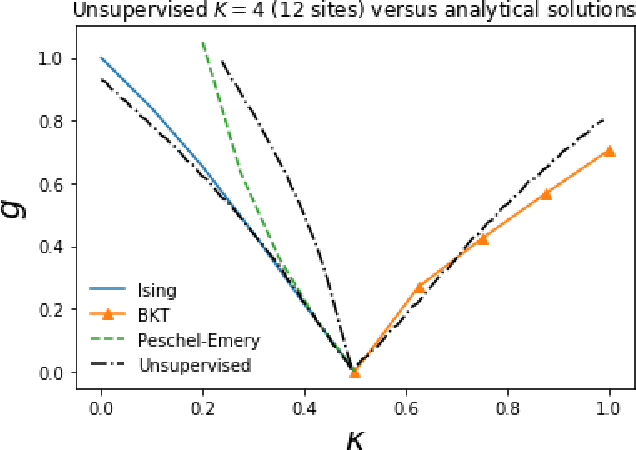
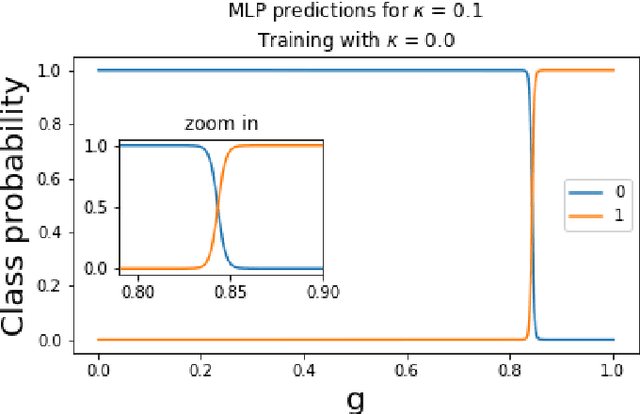
The classification of phase transitions is a central and challenging task in condensed matter physics. Typically, it relies on the identification of order parameters and the analysis of singularities in the free energy and its derivatives. Here, we propose an alternative framework to identify quantum phase transitions, employing both unsupervised and supervised machine learning techniques. Using the axial next-nearest neighbor Ising (ANNNI) model as a benchmark, we show how unsupervised learning can detect three phases (ferromagnetic, paramagnetic, and a cluster of the antiphase with the floating phase) as well as two distinct regions within the paramagnetic phase. Employing supervised learning we show that transfer learning becomes possible: a machine trained only with nearest-neighbour interactions can learn to identify a new type of phase occurring when next-nearest-neighbour interactions are introduced. All our results rely on few and low dimensional input data (up to twelve lattice sites), thus providing a computational friendly and general framework for the study of phase transitions in many-body systems.

Machine learning non-local correlations

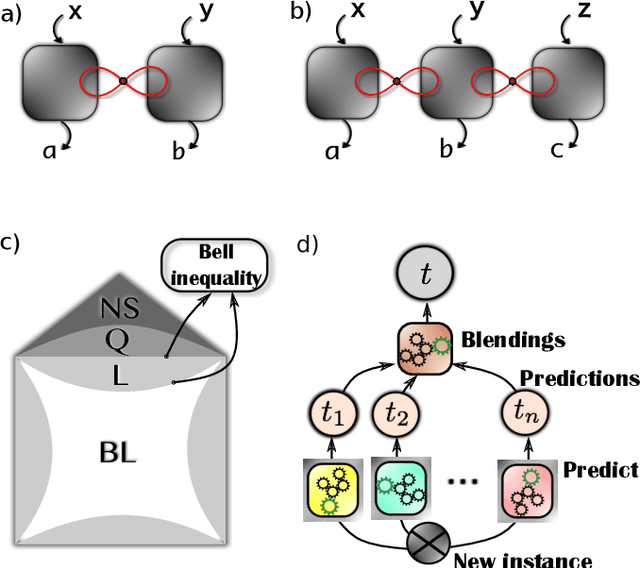
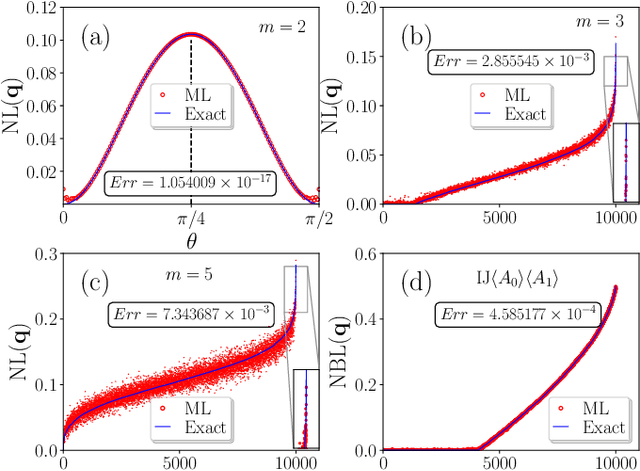
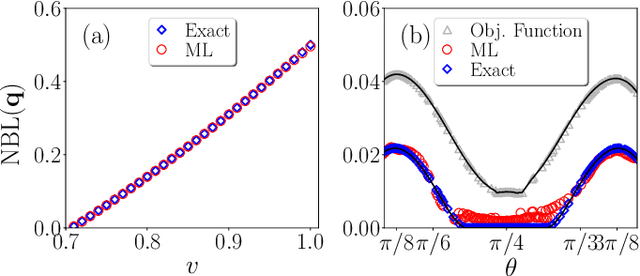
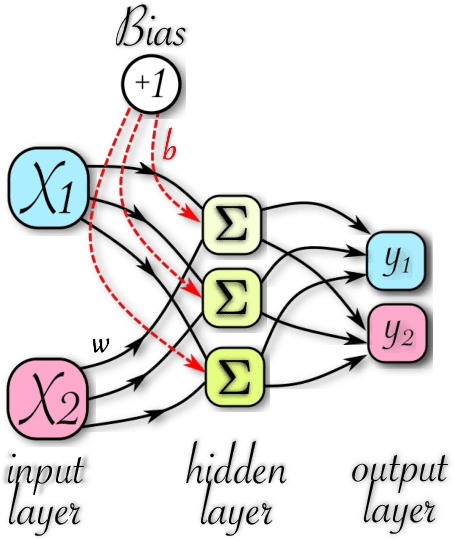
The ability to witness non-local correlations lies at the core of foundational aspects of quantum mechanics and its application in the processing of information. Commonly, this is achieved via the violation of Bell inequalities. Unfortunately, however, their systematic derivation quickly becomes unfeasible as the scenario of interest grows in complexity. To cope with that, we propose here a machine learning approach for the detection and quantification of non-locality. It consists of an ensemble of multilayer perceptrons blended with genetic algorithms achieving a high performance in a number of relevant Bell scenarios. Our results offer a novel method and a proof-of-principle for the relevance of machine learning for understanding non-locality.

Semidefinite tests for latent causal structures

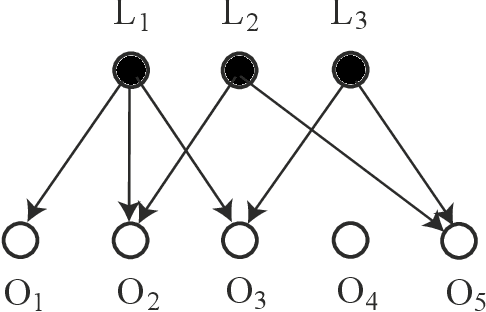
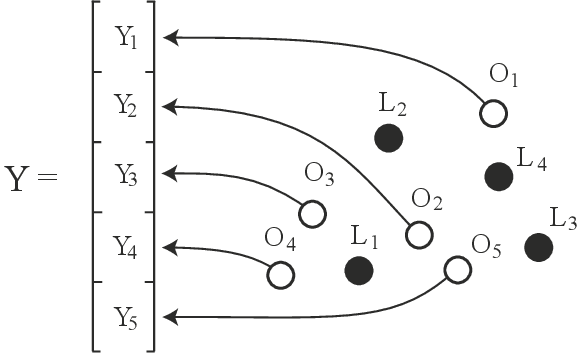
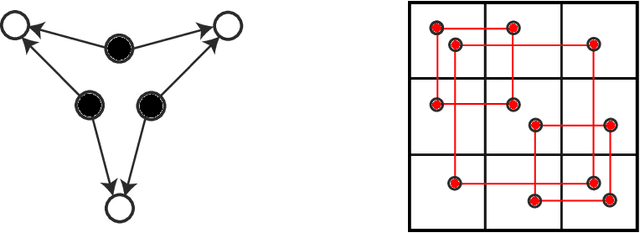
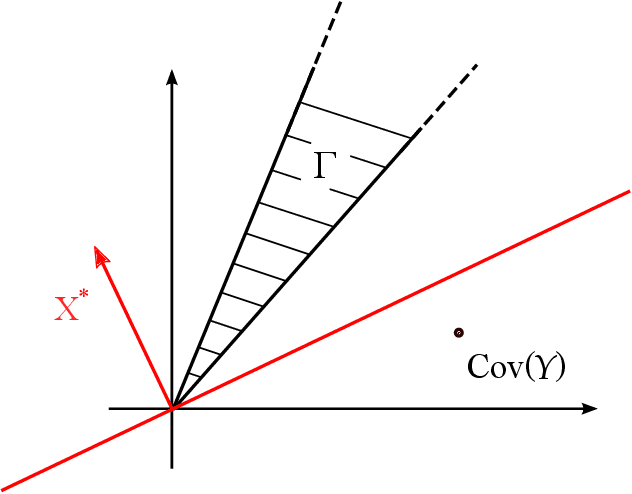
Testing whether a probability distribution is compatible with a given Bayesian network is a fundamental task in the field of causal inference, where Bayesian networks model causal relations. Here we consider the class of causal structures where all correlations between observed quantities are solely due to the influence from latent variables. We show that each model of this type imposes a certain signature on the observable covariance matrix in terms of a particular decomposition into positive semidefinite components. This signature, and thus the underlying hypothetical latent structure, can be tested in a computationally efficient manner via semidefinite programming. This stands in stark contrast with the algebraic geometric tools required if the full observable probability distribution is taken into account. The semidefinite test is compared with tests based on entropic inequalities.

A unifying framework for relaxations of the causal assumptions in Bell's theorem

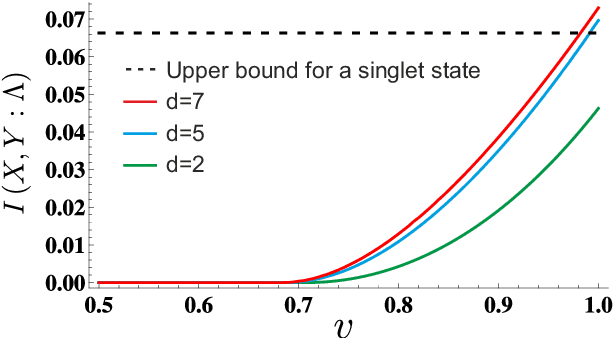
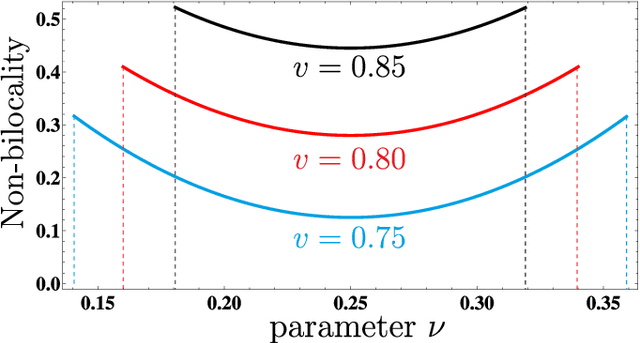
Bell's Theorem shows that quantum mechanical correlations can violate the constraints that the causal structure of certain experiments impose on any classical explanation. It is thus natural to ask to which degree the causal assumptions -- e.g. locality or measurement independence -- have to be relaxed in order to allow for a classical description of such experiments. Here, we develop a conceptual and computational framework for treating this problem. We employ the language of Bayesian networks to systematically construct alternative causal structures and bound the degree of relaxation using quantitative measures that originate from the mathematical theory of causality. The main technical insight is that the resulting problems can often be expressed as computationally tractable linear programs. We demonstrate the versatility of the framework by applying it to a variety of scenarios, ranging from relaxations of the measurement independence, locality and bilocality assumptions, to a novel causal interpretation of CHSH inequality violations.