An Efficient Quantum Classifier Based on Hamiltonian Representations

Quantum machine learning (QML) is a discipline that seeks to transfer the advantages of quantum computing to data-driven tasks. However, many studies rely on toy datasets or heavy feature reduction, raising concerns about their scalability. Progress is further hindered by hardware limitations and the significant costs of encoding dense vector representations on quantum devices. To address these challenges, we propose an efficient approach called Hamiltonian classifier that circumvents the costs associated with data encoding by mapping inputs to a finite set of Pauli strings and computing predictions as their expectation values. In addition, we introduce two classifier variants with different scaling in terms of parameters and sample complexity. We evaluate our approach on text and image classification tasks, against well-established classical and quantum models. The Hamiltonian classifier delivers performance comparable to or better than these methods. Notably, our method achieves logarithmic complexity in both qubits and quantum gates, making it well-suited for large-scale, real-world applications. We make our implementation available on GitHub.

Causal inference with imperfect instrumental variables

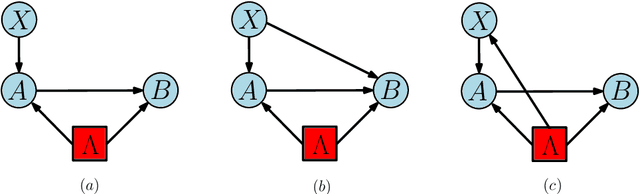
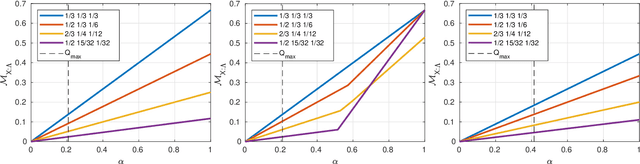
Instrumental variables allow for quantification of cause and effect relationships even in the absence of interventions. To achieve this, a number of causal assumptions must be met, the most important of which is the independence assumption, which states that the instrument and any confounding factor must be independent. However, if this independence condition is not met, can we still work with imperfect instrumental variables? Imperfect instruments can manifest themselves by violations of the instrumental inequalities that constrain the set of correlations in the scenario. In this paper, we establish a quantitative relationship between such violations of instrumental inequalities and the minimal amount of measurement dependence required to explain them. As a result, we provide adapted inequalities that are valid in the presence of a relaxed measurement dependence assumption in the instrumental scenario. This allows for the adaptation of existing and new lower bounds on the average causal effect for instrumental scenarios with binary outcomes. Finally, we discuss our findings in the context of quantum mechanics.

Quantifying causal influences in the presence of a quantum common cause

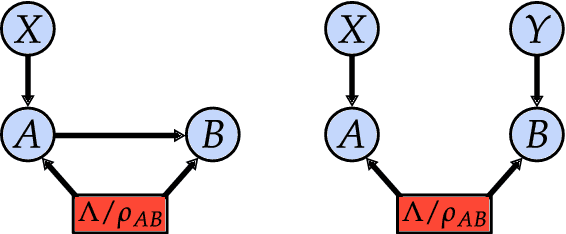
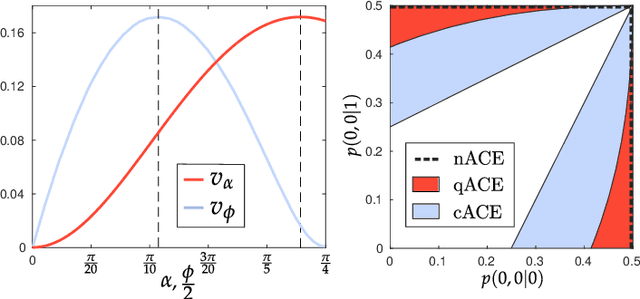
Quantum mechanics challenges our intuition on the cause-effect relations in nature. Some fundamental concepts, including Reichenbach's common cause principle or the notion of local realism, have to be reconsidered. Traditionally, this is witnessed by the violation of a Bell inequality. But are Bell inequalities the only signature of the incompatibility between quantum correlations and causality theory? Motivated by this question we introduce a general framework able to estimate causal influences between two variables, without the need of interventions and irrespectively of the classical, quantum, or even post-quantum nature of a common cause. In particular, by considering the simplest instrumental scenario -- for which violation of Bell inequalities is not possible -- we show that every pure bipartite entangled state violates the classical bounds on causal influence, thus answering in negative to the posed question and opening a new venue to explore the role of causality within quantum theory.