Causal inference with imperfect instrumental variables

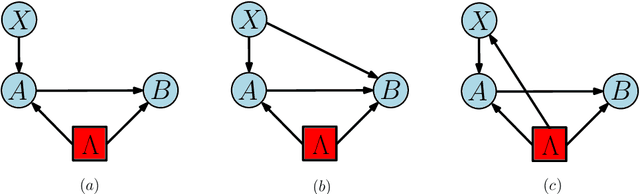
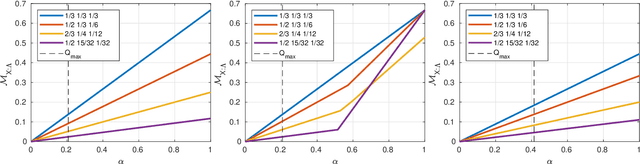
Instrumental variables allow for quantification of cause and effect relationships even in the absence of interventions. To achieve this, a number of causal assumptions must be met, the most important of which is the independence assumption, which states that the instrument and any confounding factor must be independent. However, if this independence condition is not met, can we still work with imperfect instrumental variables? Imperfect instruments can manifest themselves by violations of the instrumental inequalities that constrain the set of correlations in the scenario. In this paper, we establish a quantitative relationship between such violations of instrumental inequalities and the minimal amount of measurement dependence required to explain them. As a result, we provide adapted inequalities that are valid in the presence of a relaxed measurement dependence assumption in the instrumental scenario. This allows for the adaptation of existing and new lower bounds on the average causal effect for instrumental scenarios with binary outcomes. Finally, we discuss our findings in the context of quantum mechanics.

Causal networks and freedom of choice in Bell's theorem

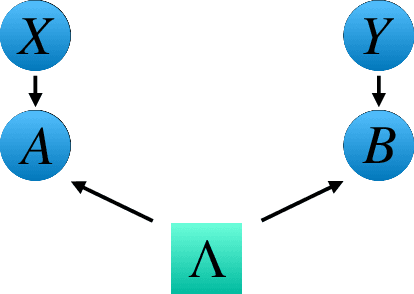
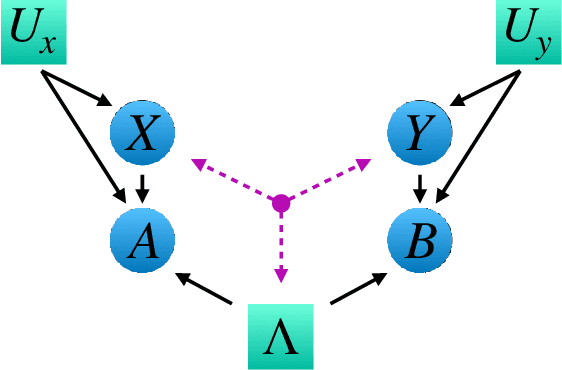
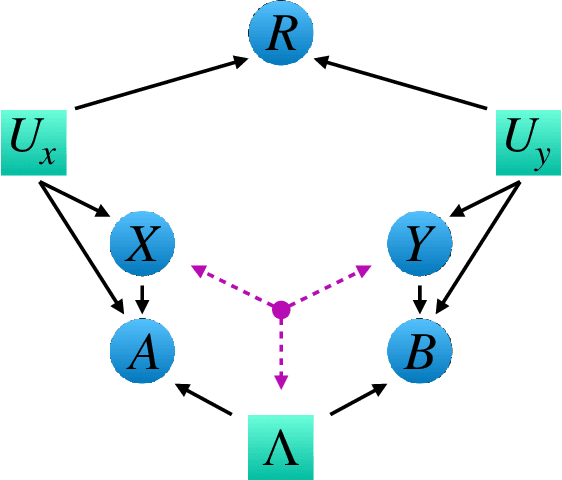
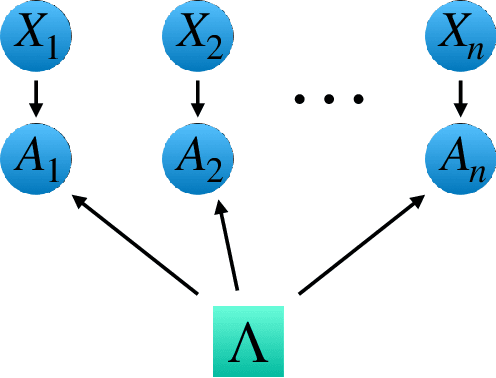
Bell's theorem is typically understood as the proof that quantum theory is incompatible with local hidden variable models. More generally, we can see the violation of a Bell inequality as witnessing the impossibility of explaining quantum correlations with classical causal models. The violation of a Bell inequality, however, does not exclude classical models where some level of measurement dependence is allowed, that is, the choice made by observers can be correlated with the source generating the systems to be measured. Here we show that the level of measurement dependence can be quantitatively upper bounded if we arrange the Bell test within a network. Furthermore, we also prove that these results can be adapted in order to derive non-linear Bell inequalities for a large class of causal networks and to identify quantumly realizable correlations which violate them.