Causal networks and freedom of choice in Bell's theorem

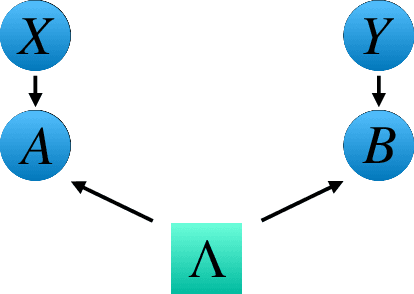
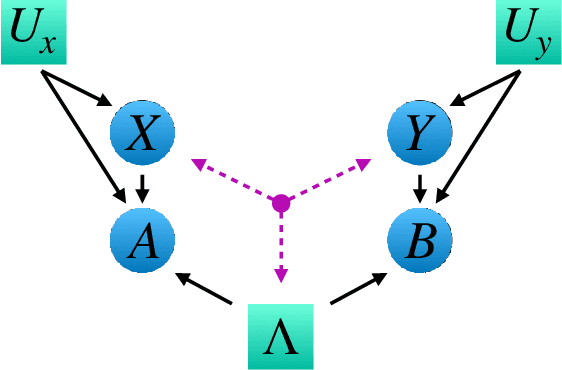
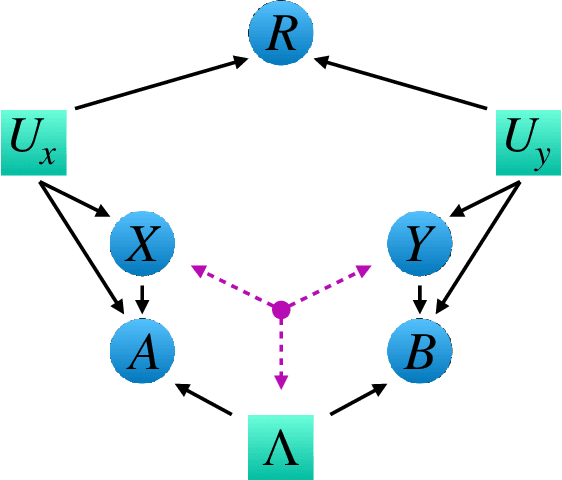
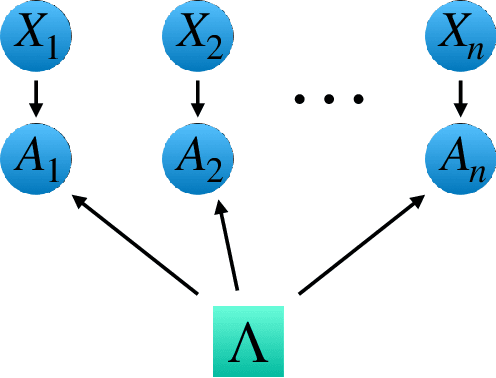
Bell's theorem is typically understood as the proof that quantum theory is incompatible with local hidden variable models. More generally, we can see the violation of a Bell inequality as witnessing the impossibility of explaining quantum correlations with classical causal models. The violation of a Bell inequality, however, does not exclude classical models where some level of measurement dependence is allowed, that is, the choice made by observers can be correlated with the source generating the systems to be measured. Here we show that the level of measurement dependence can be quantitatively upper bounded if we arrange the Bell test within a network. Furthermore, we also prove that these results can be adapted in order to derive non-linear Bell inequalities for a large class of causal networks and to identify quantumly realizable correlations which violate them.

Pattern recognition techniques for Boson Sampling validation

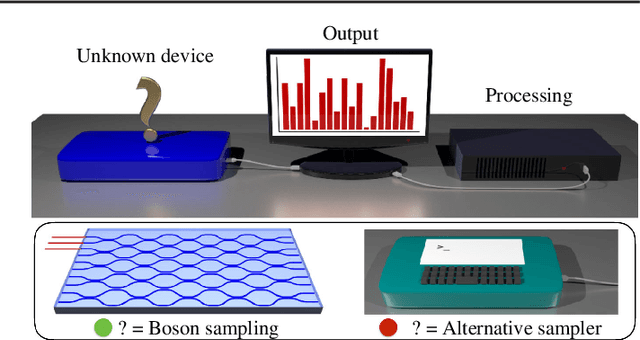
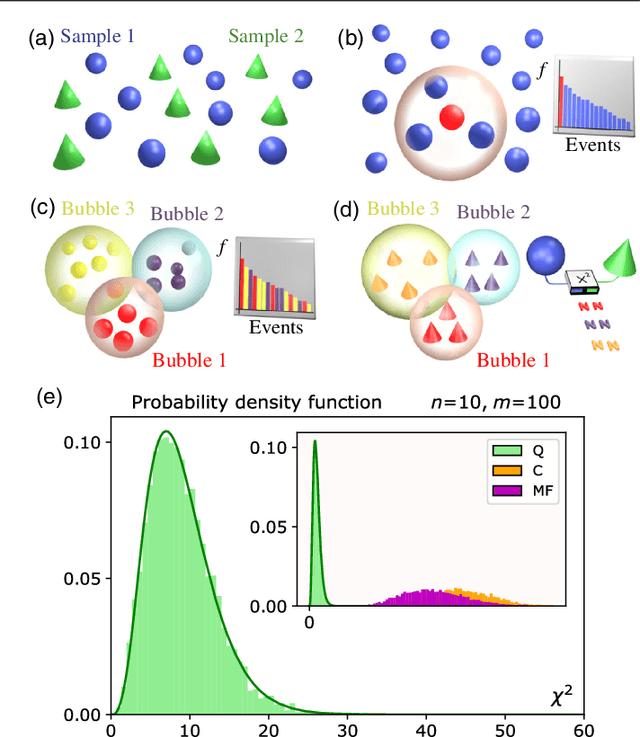
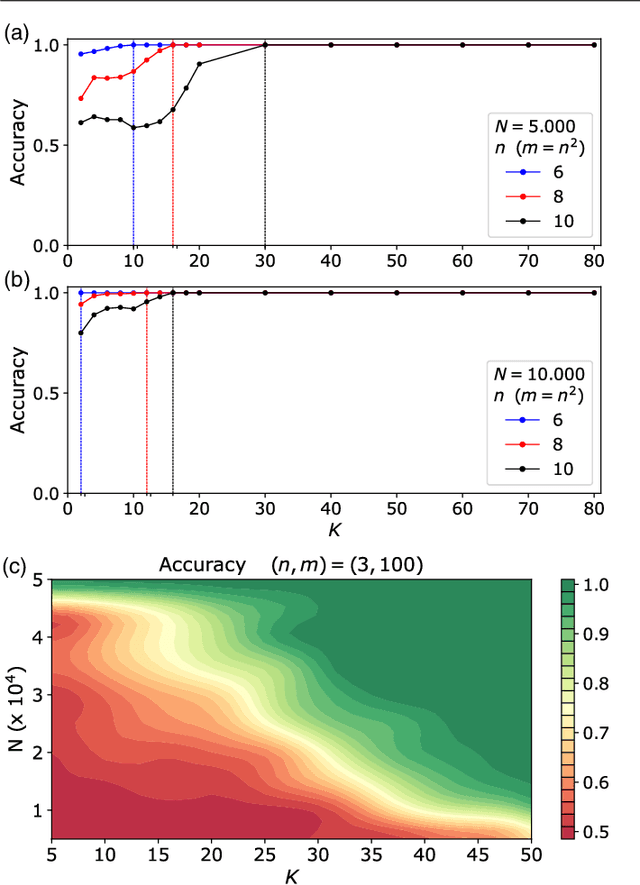
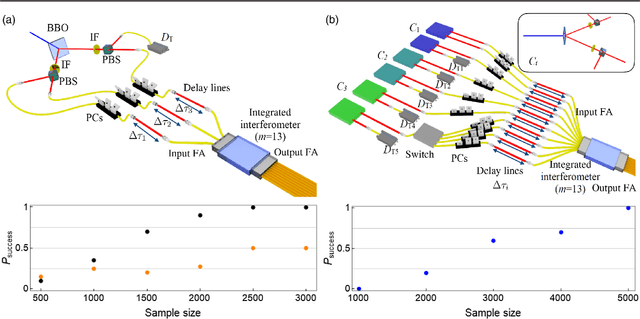
The difficulty of validating large-scale quantum devices, such as Boson Samplers, poses a major challenge for any research program that aims to show quantum advantages over classical hardware. To address this problem, we propose a novel data-driven approach wherein models are trained to identify common pathologies using unsupervised machine learning methods. We illustrate this idea by training a classifier that exploits K-means clustering to distinguish between Boson Samplers that use indistinguishable photons from those that do not. We train the model on numerical simulations of small-scale Boson Samplers and then validate the pattern recognition technique on larger numerical simulations as well as on photonic chips in both traditional Boson Sampling and scattershot experiments. The effectiveness of such method relies on particle-type-dependent internal correlations present in the output distributions. This approach performs substantially better on the test data than previous methods and underscores the ability to further generalize its operation beyond the scope of the examples that it was trained on.

Experimental learning of quantum states

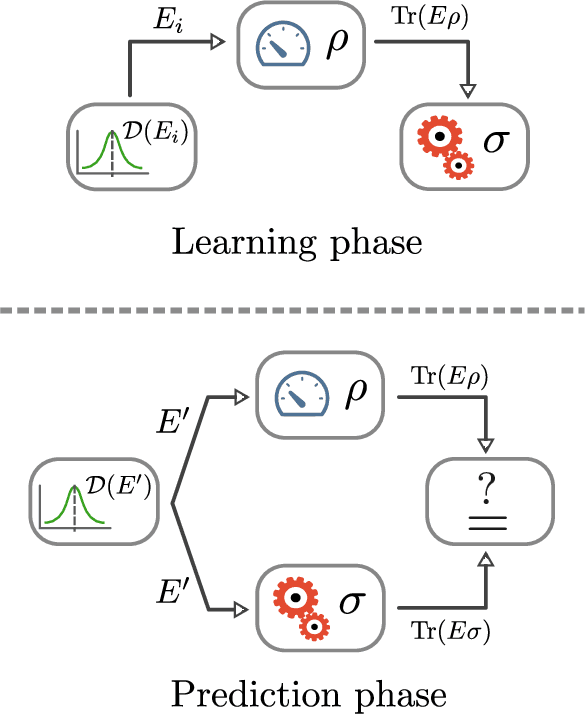
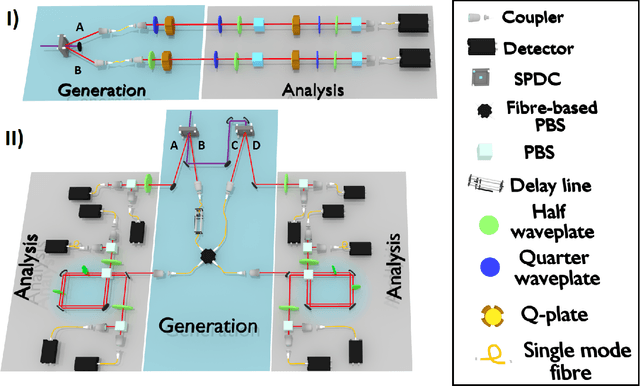
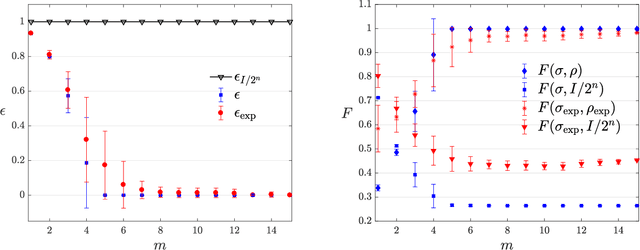
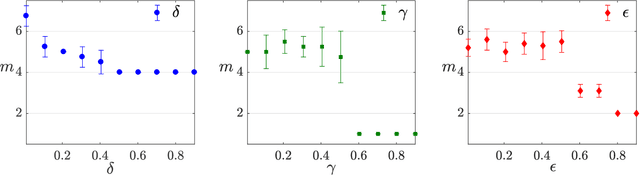
The number of parameters describing a quantum state is well known to grow exponentially with the number of particles. This scaling clearly limits our ability to do tomography to systems with no more than a few qubits and has been used to argue against the universal validity of quantum mechanics itself. However, from a computational learning theory perspective, it can be shown that, in a probabilistic setting, quantum states can be approximately learned using only a linear number of measurements. Here we experimentally demonstrate this linear scaling in optical systems with up to 6 qubits. Our results highlight the power of computational learning theory to investigate quantum information, provide the first experimental demonstration that quantum states can be "probably approximately learned" with access to a number of copies of the state that scales linearly with the number of qubits, and pave the way to probing quantum states at new, larger scales.