Quantum Model Learning Agent: characterisation of quantum systems through machine learning

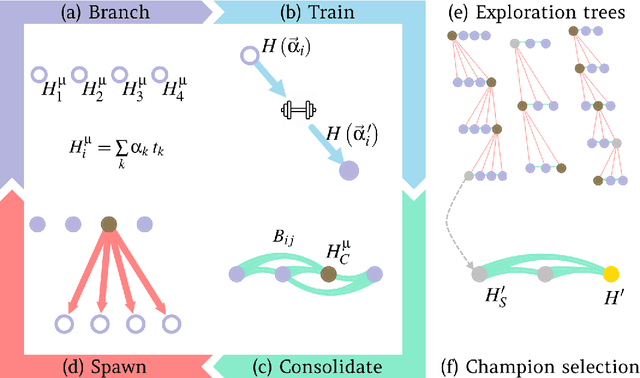
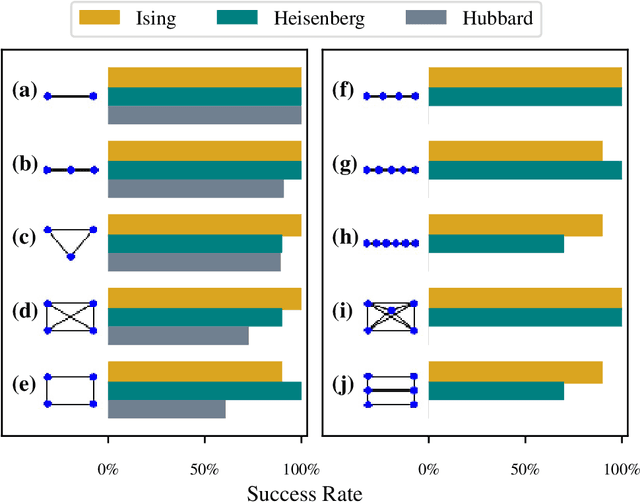
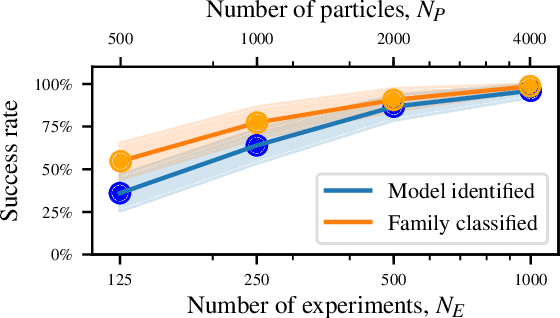
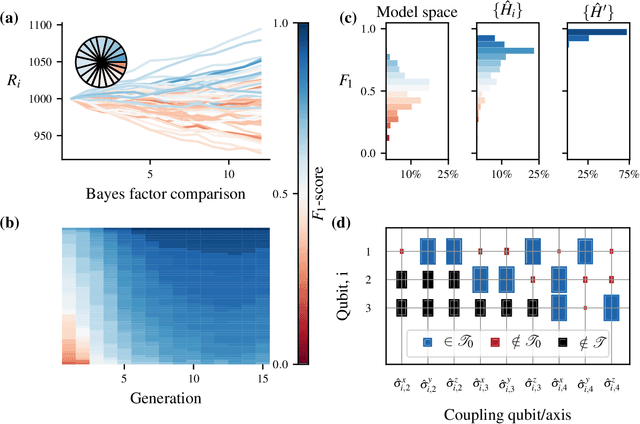
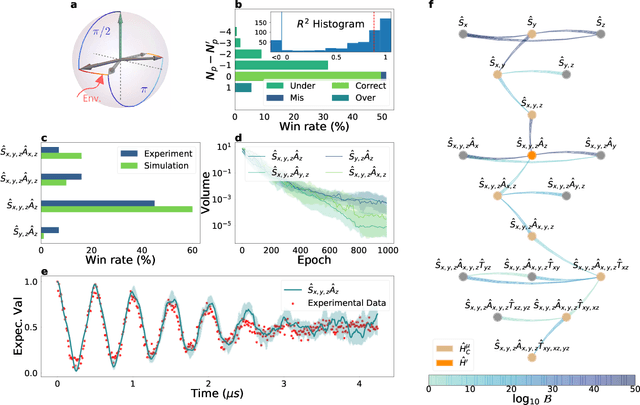
Accurate models of real quantum systems are important for investigating their behaviour, yet are difficult to distill empirically. Here, we report an algorithm -- the Quantum Model Learning Agent (QMLA) -- to reverse engineer Hamiltonian descriptions of a target system. We test the performance of QMLA on a number of simulated experiments, demonstrating several mechanisms for the design of candidate Hamiltonian models and simultaneously entertaining numerous hypotheses about the nature of the physical interactions governing the system under study. QMLA is shown to identify the true model in the majority of instances, when provided with limited a priori information, and control of the experimental setup. Our protocol can explore Ising, Heisenberg and Hubbard families of models in parallel, reliably identifying the family which best describes the system dynamics. We demonstrate QMLA operating on large model spaces by incorporating a genetic algorithm to formulate new hypothetical models. The selection of models whose features propagate to the next generation is based upon an objective function inspired by the Elo rating scheme, typically used to rate competitors in games such as chess and football. In all instances, our protocol finds models that exhibit $F_1$-score $\geq 0.88$ when compared with the true model, and it precisely identifies the true model in 72% of cases, whilst exploring a space of over $250,000$ potential models. By testing which interactions actually occur in the target system, QMLA is a viable tool for both the exploration of fundamental physics and the characterisation and calibration of quantum devices.

Entanglement Induced Barren Plateaus

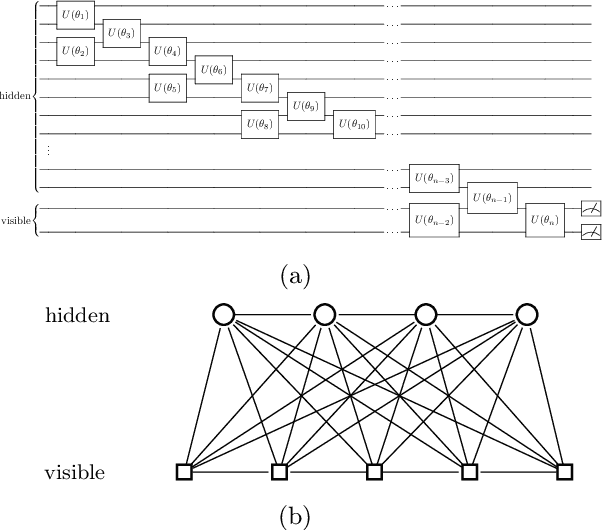
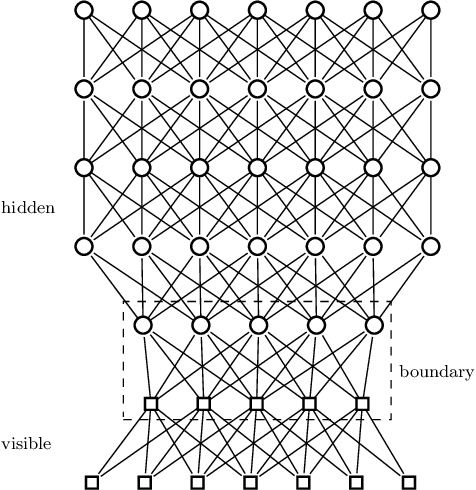
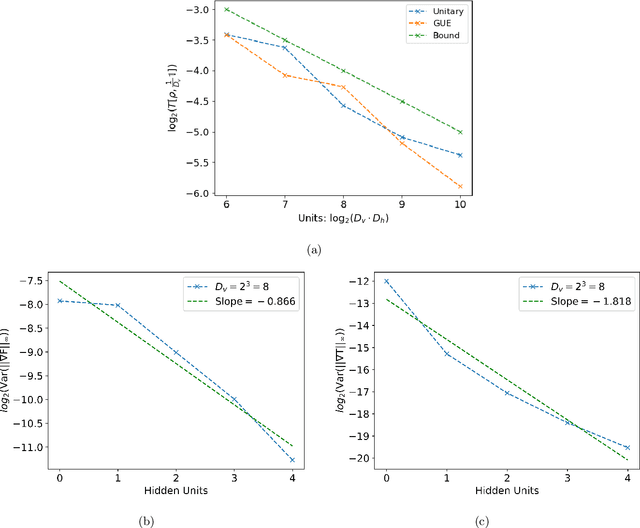
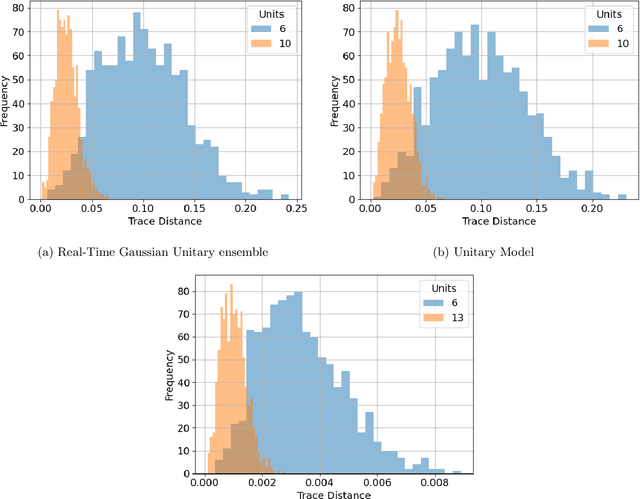
We argue that an excess in entanglement between the visible and hidden units in a Quantum Neural Network can hinder learning. In particular, we show that quantum neural networks that satisfy a volume-law in the entanglement entropy will give rise to models not suitable for learning with high probability. Using arguments from quantum thermodynamics, we then show that this volume law is typical and that there exists a barren plateau in the optimization landscape due to entanglement. More precisely, we show that for any bounded objective function on the visible layers, the Lipshitz constants of the expectation value of that objective function will scale inversely with the dimension of the hidden-subsystem with high probability. We show how this can cause both gradient descent and gradient-free methods to fail. We note that similar problems can happen with quantum Boltzmann machines, although stronger assumptions on the coupling between the hidden/visible subspaces are necessary. We highlight how pretraining such generative models may provide a way to navigate these barren plateaus.

Learning models of quantum systems from experiments

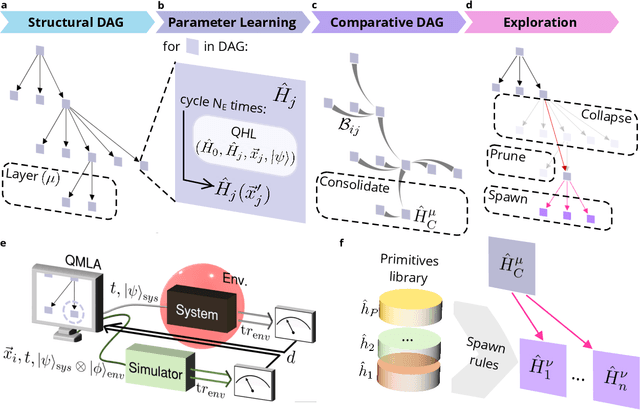
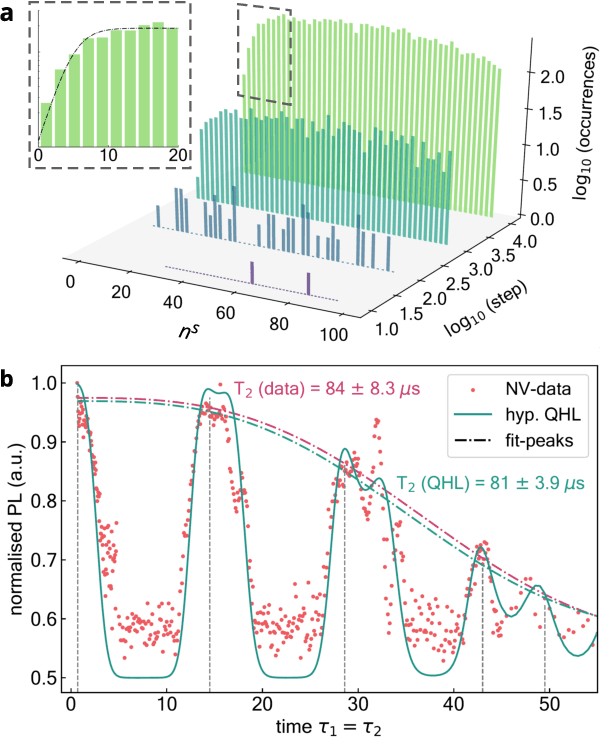
An isolated system of interacting quantum particles is described by a Hamiltonian operator. Hamiltonian models underpin the study and analysis of physical and chemical processes throughout science and industry, so it is crucial they are faithful to the system they represent. However, formulating and testing Hamiltonian models of quantum systems from experimental data is difficult because it is impossible to directly observe which interactions the quantum system is subject to. Here, we propose and demonstrate an approach to retrieving a Hamiltonian model from experiments, using unsupervised machine learning. We test our methods experimentally on an electron spin in a nitrogen-vacancy interacting with its spin bath environment, and numerically, finding success rates up to 86%. By building agents capable of learning science, which recover meaningful representations, we can gain further insight on the physics of quantum systems.

Generative training of quantum Boltzmann machines with hidden units

In this article we provide a method for fully quantum generative training of quantum Boltzmann machines with both visible and hidden units while using quantum relative entropy as an objective. This is significant because prior methods were not able to do so due to mathematical challenges posed by the gradient evaluation. We present two novel methods for solving this problem. The first proposal addresses it, for a class of restricted quantum Boltzmann machines with mutually commuting Hamiltonians on the hidden units, by using a variational upper bound on the quantum relative entropy. The second one uses high-order divided difference methods and linear-combinations of unitaries to approximate the exact gradient of the relative entropy for a generic quantum Boltzmann machine. Both methods are efficient under the assumption that Gibbs state preparation is efficient and that the Hamiltonian are given by a sparse row-computable matrix.

Quantum Machine Learning

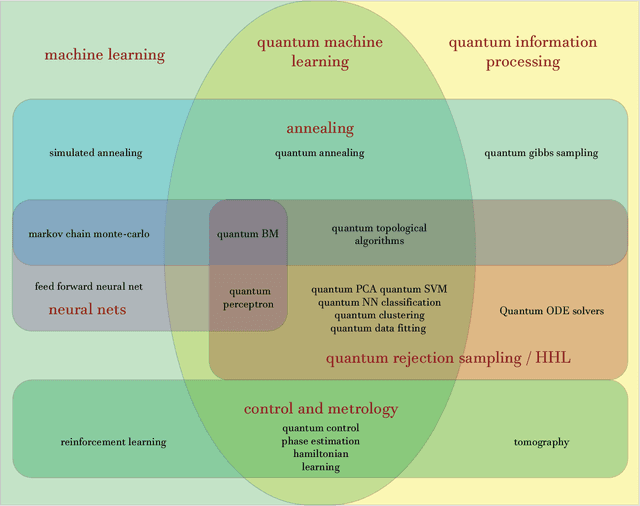
Fuelled by increasing computer power and algorithmic advances, machine learning techniques have become powerful tools for finding patterns in data. Since quantum systems produce counter-intuitive patterns believed not to be efficiently produced by classical systems, it is reasonable to postulate that quantum computers may outperform classical computers on machine learning tasks. The field of quantum machine learning explores how to devise and implement concrete quantum software that offers such advantages. Recent work has made clear that the hardware and software challenges are still considerable but has also opened paths towards solutions.

Experimental Phase Estimation Enhanced By Machine Learning

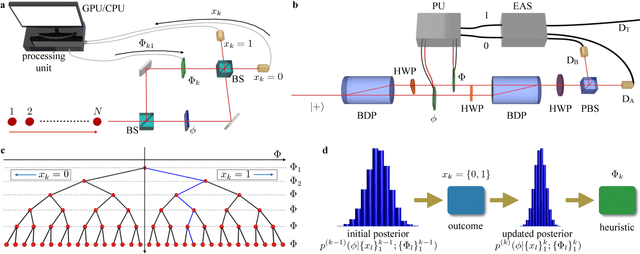
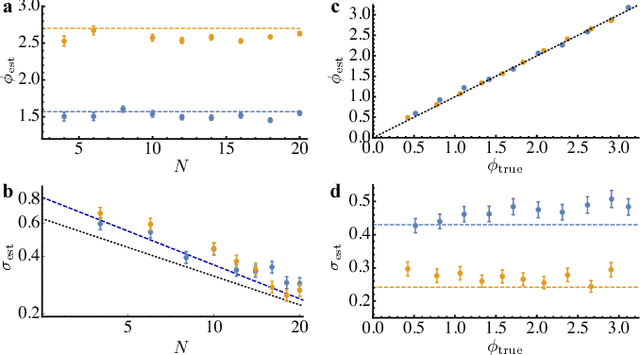
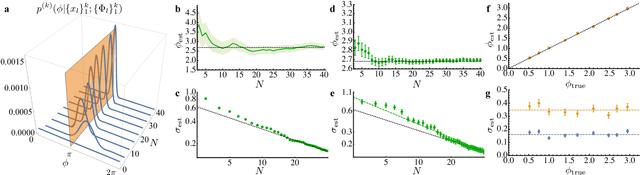
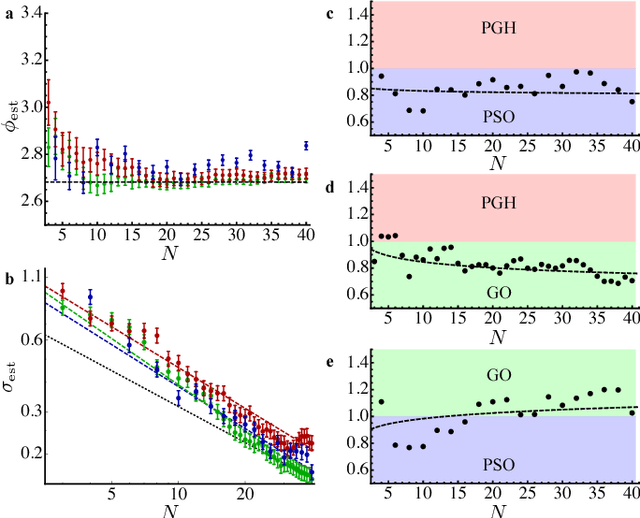
Phase estimation protocols provide a fundamental benchmark for the field of quantum metrology. The latter represents one of the most relevant applications of quantum theory, potentially enabling the capability of measuring unknown physical parameters with improved precision over classical strategies. Within this context, most theoretical and experimental studies have focused on determining the fundamental bounds and how to achieve them in the asymptotic regime where a large number of resources is employed. However, in most applications it is necessary to achieve optimal precisions by performing only a limited number of measurements. To this end, machine learning techniques can be applied as a powerful optimization tool. Here, we implement experimentally single-photon adaptive phase estimation protocols enhanced by machine learning, showing the capability of reaching optimal precision after a small number of trials. In particular, we introduce a new approach for Bayesian estimation that exhibit best performances for very low number of photons N. Furthermore, we study the resilience to noise of the tested methods, showing that the optimized Bayesian approach is very robust in the presence of imperfections. Application of this methodology can be envisaged in the more general multiparameter case, that represents a paradigmatic scenario for several tasks including imaging or Hamiltonian learning.

Pattern recognition techniques for Boson Sampling validation

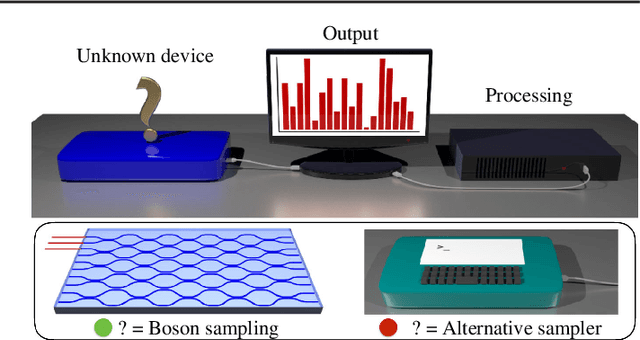
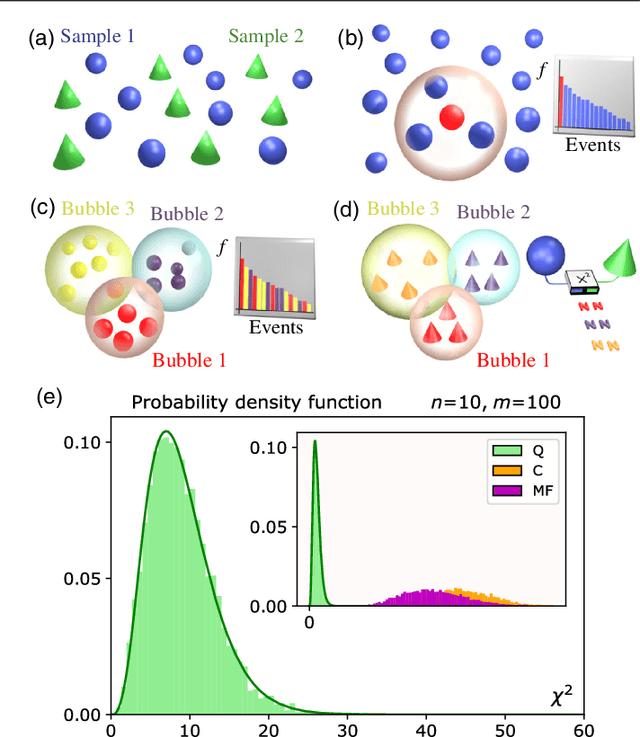
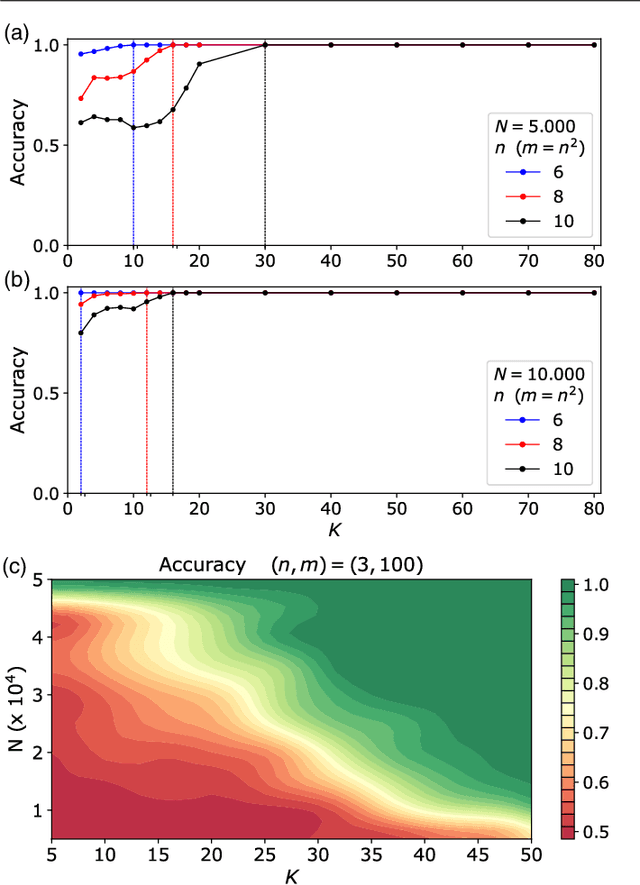
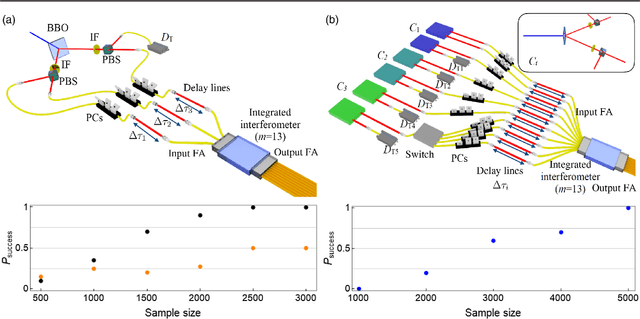
The difficulty of validating large-scale quantum devices, such as Boson Samplers, poses a major challenge for any research program that aims to show quantum advantages over classical hardware. To address this problem, we propose a novel data-driven approach wherein models are trained to identify common pathologies using unsupervised machine learning methods. We illustrate this idea by training a classifier that exploits K-means clustering to distinguish between Boson Samplers that use indistinguishable photons from those that do not. We train the model on numerical simulations of small-scale Boson Samplers and then validate the pattern recognition technique on larger numerical simulations as well as on photonic chips in both traditional Boson Sampling and scattershot experiments. The effectiveness of such method relies on particle-type-dependent internal correlations present in the output distributions. This approach performs substantially better on the test data than previous methods and underscores the ability to further generalize its operation beyond the scope of the examples that it was trained on.

Hardening Quantum Machine Learning Against Adversaries

Security for machine learning has begun to become a serious issue for present day applications. An important question remaining is whether emerging quantum technologies will help or hinder the security of machine learning. Here we discuss a number of ways that quantum information can be used to help make quantum classifiers more secure or private. In particular, we demonstrate a form of robust principal component analysis that, under some circumstances, can provide an exponential speedup relative to robust methods used at present. To demonstrate this approach we introduce a linear combinations of unitaries Hamiltonian simulation method that we show functions when given an imprecise Hamiltonian oracle, which may be of independent interest. We also introduce a new quantum approach for bagging and boosting that can use quantum superposition over the classifiers or splits of the training set to aggregate over many more models than would be possible classically. Finally, we provide a private form of $k$--means clustering that can be used to prevent an all powerful adversary from learning more than a small fraction of a bit from any user. These examples show the role that quantum technologies can play in the security of ML and vice versa. This illustrates that quantum computing can provide useful advantages to machine learning apart from speedups.

Quantum Perceptron Models

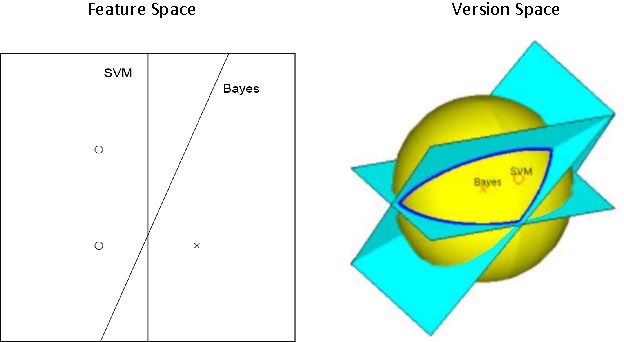
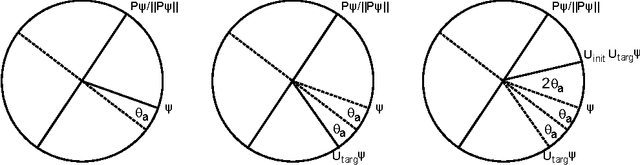
We demonstrate how quantum computation can provide non-trivial improvements in the computational and statistical complexity of the perceptron model. We develop two quantum algorithms for perceptron learning. The first algorithm exploits quantum information processing to determine a separating hyperplane using a number of steps sublinear in the number of data points $N$, namely $O(\sqrt{N})$. The second algorithm illustrates how the classical mistake bound of $O(\frac{1}{\gamma^2})$ can be further improved to $O(\frac{1}{\sqrt{\gamma}})$ through quantum means, where $\gamma$ denotes the margin. Such improvements are achieved through the application of quantum amplitude amplification to the version space interpretation of the perceptron model.

Partial Reinitialisation for Optimisers

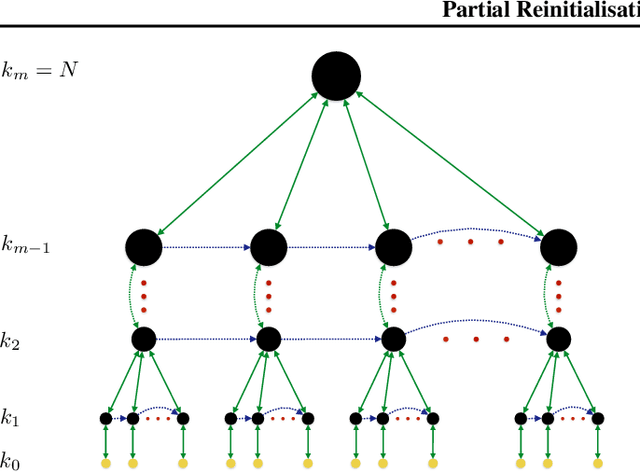
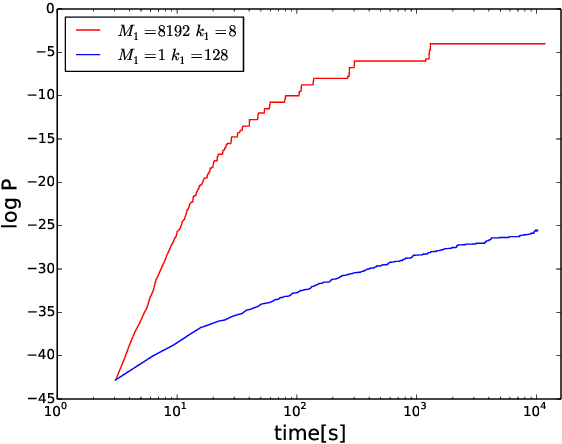
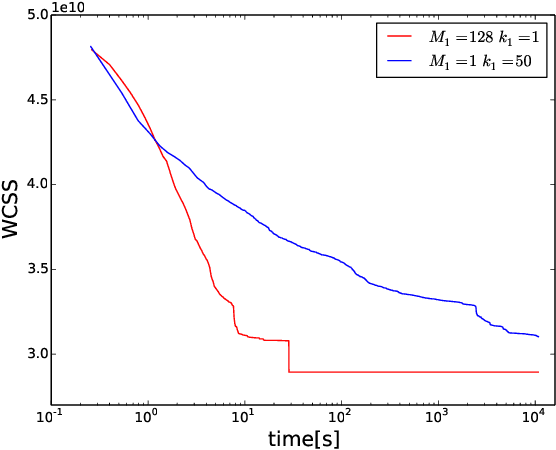
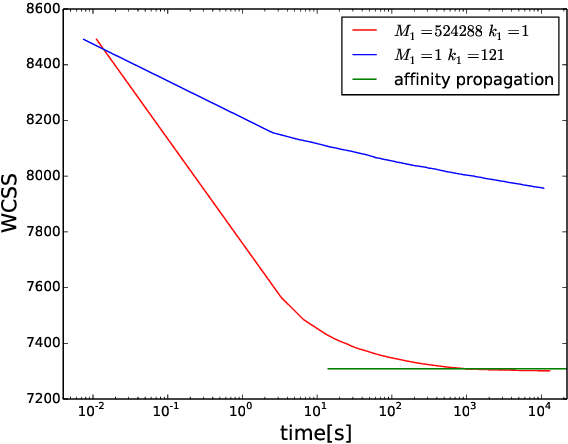
Heuristic optimisers which search for an optimal configuration of variables relative to an objective function often get stuck in local optima where the algorithm is unable to find further improvement. The standard approach to circumvent this problem involves periodically restarting the algorithm from random initial configurations when no further improvement can be found. We propose a method of partial reinitialization, whereby, in an attempt to find a better solution, only sub-sets of variables are re-initialised rather than the whole configuration. Much of the information gained from previous runs is hence retained. This leads to significant improvements in the quality of the solution found in a given time for a variety of optimisation problems in machine learning.