Matthias Troyer
A Fast MR Fingerprinting Simulator for Direct Error Estimation and Sequence Optimization
May 25, 2021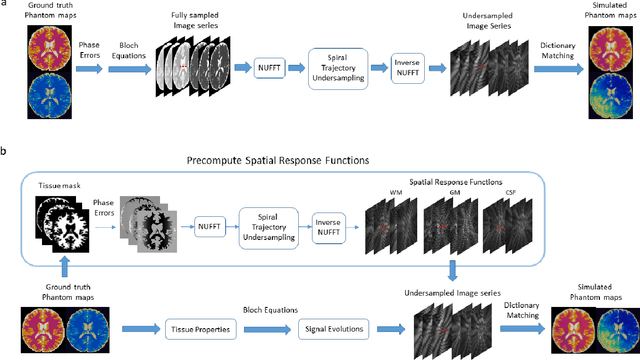
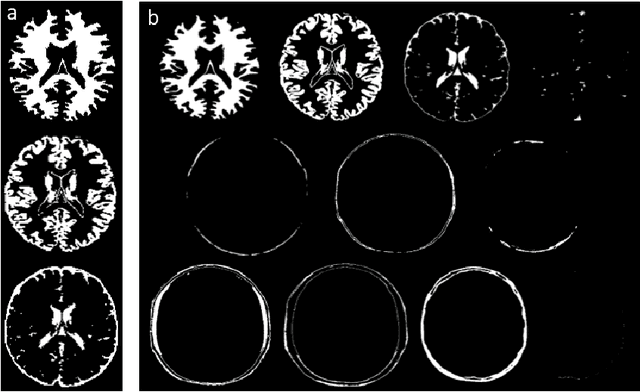
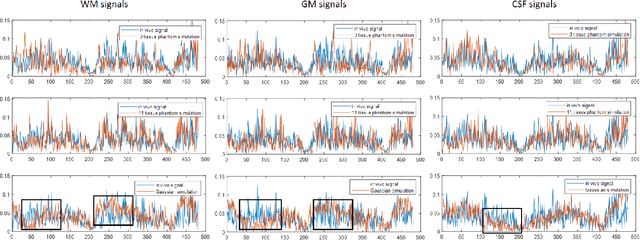

Abstract:MR Fingerprinting is a novel quantitative MR technique that could simultaneously provide multiple tissue property maps. When optimizing MRF scans, modeling undersampling errors and field imperfections in cost functions will make the optimization results more practical and robust. However, this process is computationally expensive and impractical for sequence optimization algorithms when MRF signal evolutions need to be generated for each optimization iteration. Here, we introduce a fast MRF simulator to simulate aliased images from actual scan scenarios including undersampling and system imperfections, which substantially reduces computational time and allows for direct error estimation and efficient sequence optimization. By constraining the total number of tissues present in a brain phantom, MRF signals from highly undersampled scans can be simulated as the product of the spatial response functions based on sampling patterns and sequence-dependent temporal functions. During optimization, the spatial response function is independent of sequence design and does not need to be recalculated. We evaluate the performance and computational speed of the proposed approach by simulations and in vivo experiments. We also demonstrate the power of applying the simulator in MRF sequence optimization. The simulation results from the proposed method closely approximate the signals and MRF maps from in vivo scans, with 158 times shorter processing time than the conventional simulation method using Non-uniform Fourier transform. Incorporating the proposed simulator in the MRF optimization framework makes direct estimation of undersampling errors during the optimization process feasible, and provide optimized MRF sequences that are robust against undersampling factors and system inhomogeneity.
Partial Reinitialisation for Optimisers
Dec 09, 2015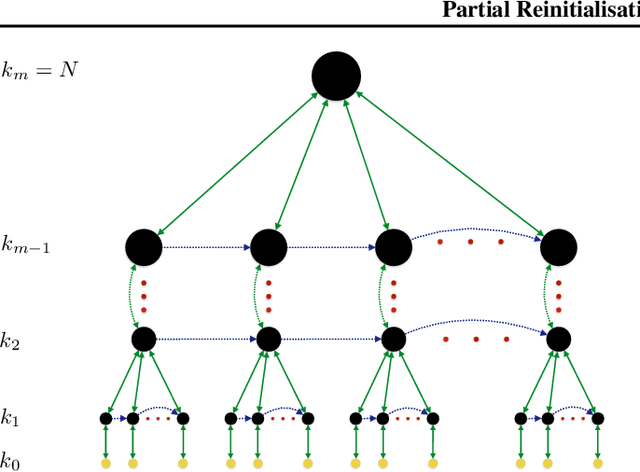
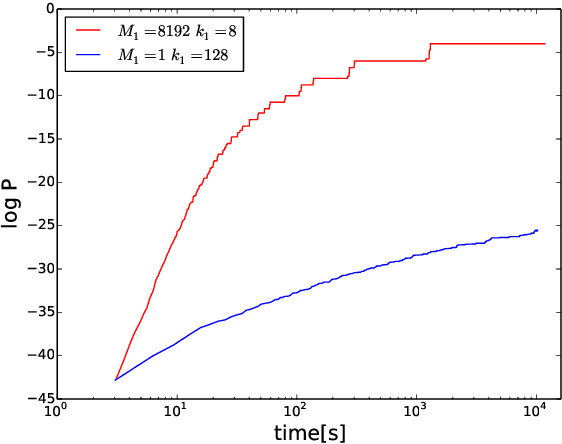
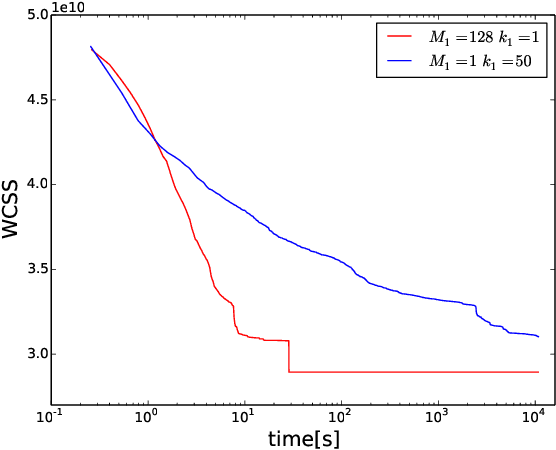
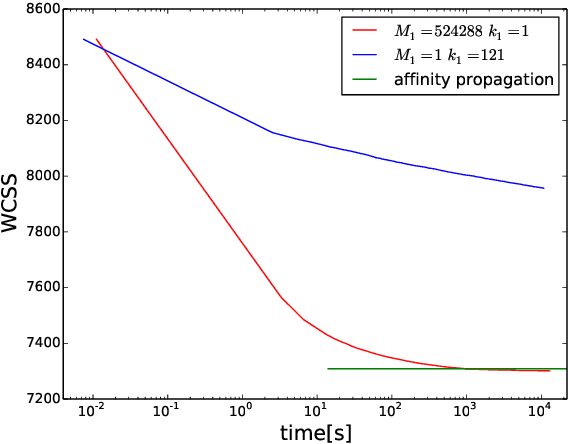
Abstract:Heuristic optimisers which search for an optimal configuration of variables relative to an objective function often get stuck in local optima where the algorithm is unable to find further improvement. The standard approach to circumvent this problem involves periodically restarting the algorithm from random initial configurations when no further improvement can be found. We propose a method of partial reinitialization, whereby, in an attempt to find a better solution, only sub-sets of variables are re-initialised rather than the whole configuration. Much of the information gained from previous runs is hence retained. This leads to significant improvements in the quality of the solution found in a given time for a variety of optimisation problems in machine learning.
Computational complexity and simulation of rare events of Ising spin glasses
Feb 15, 2004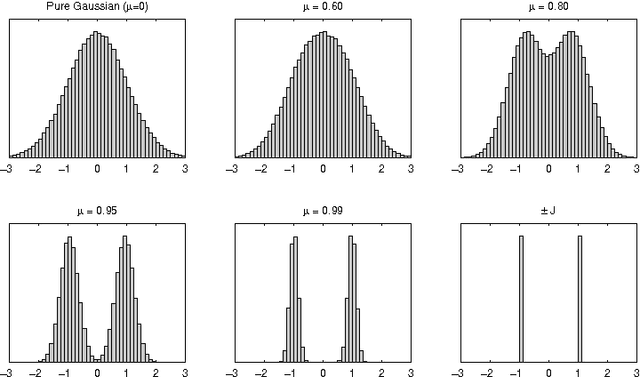
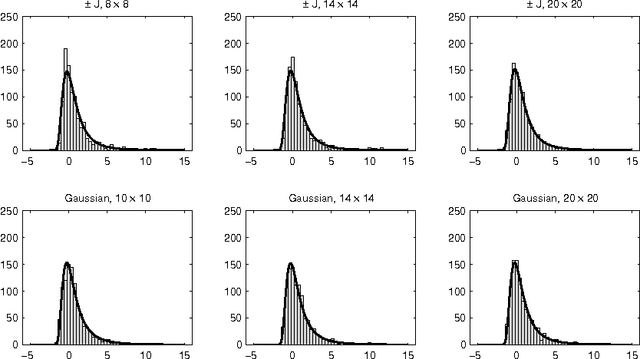
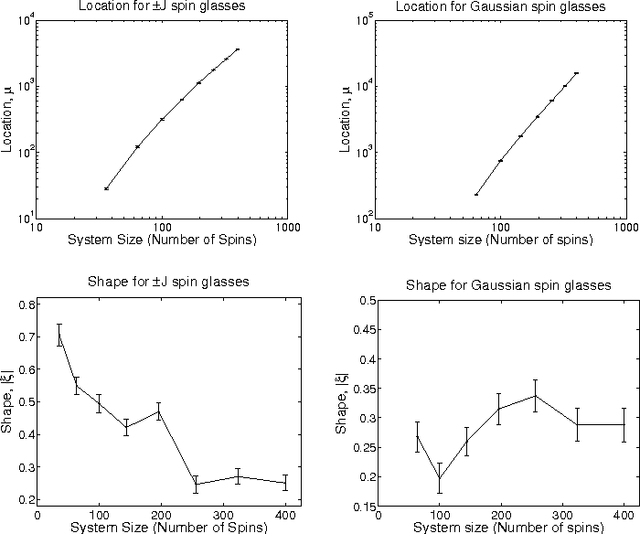
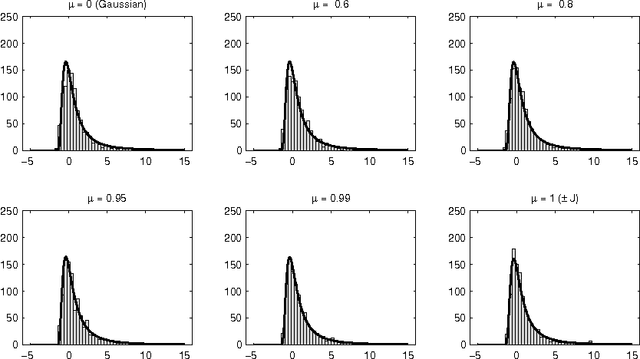
Abstract:We discuss the computational complexity of random 2D Ising spin glasses, which represent an interesting class of constraint satisfaction problems for black box optimization. Two extremal cases are considered: (1) the +/- J spin glass, and (2) the Gaussian spin glass. We also study a smooth transition between these two extremal cases. The computational complexity of all studied spin glass systems is found to be dominated by rare events of extremely hard spin glass samples. We show that complexity of all studied spin glass systems is closely related to Frechet extremal value distribution. In a hybrid algorithm that combines the hierarchical Bayesian optimization algorithm (hBOA) with a deterministic bit-flip hill climber, the number of steps performed by both the global searcher (hBOA) and the local searcher follow Frechet distributions. Nonetheless, unlike in methods based purely on local search, the parameters of these distributions confirm good scalability of hBOA with local search. We further argue that standard performance measures for optimization algorithms--such as the average number of evaluations until convergence--can be misleading. Finally, our results indicate that for highly multimodal constraint satisfaction problems, such as Ising spin glasses, recombination-based search can provide qualitatively better results than mutation-based search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge