Quantum Model Learning Agent: characterisation of quantum systems through machine learning
Paper and Code
Dec 15, 2021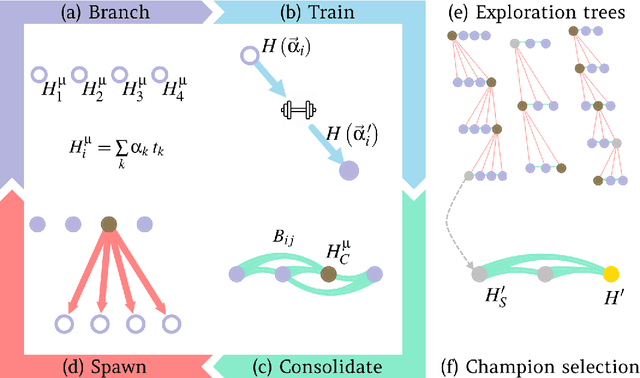
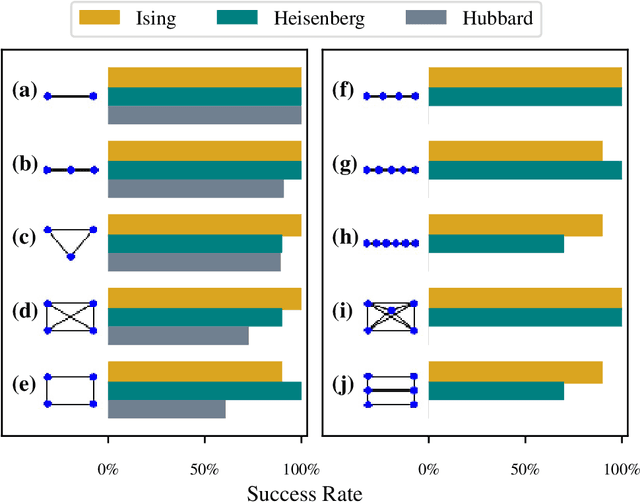
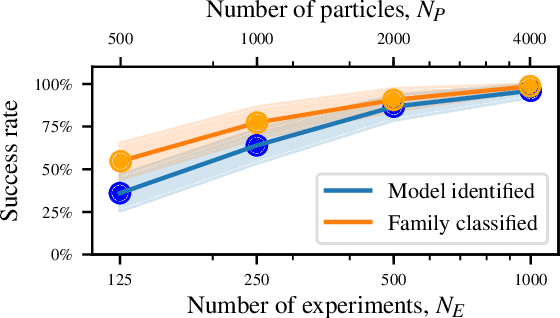
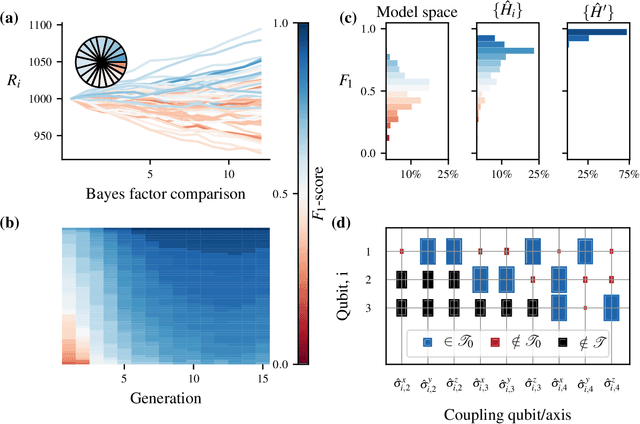
Accurate models of real quantum systems are important for investigating their behaviour, yet are difficult to distill empirically. Here, we report an algorithm -- the Quantum Model Learning Agent (QMLA) -- to reverse engineer Hamiltonian descriptions of a target system. We test the performance of QMLA on a number of simulated experiments, demonstrating several mechanisms for the design of candidate Hamiltonian models and simultaneously entertaining numerous hypotheses about the nature of the physical interactions governing the system under study. QMLA is shown to identify the true model in the majority of instances, when provided with limited a priori information, and control of the experimental setup. Our protocol can explore Ising, Heisenberg and Hubbard families of models in parallel, reliably identifying the family which best describes the system dynamics. We demonstrate QMLA operating on large model spaces by incorporating a genetic algorithm to formulate new hypothetical models. The selection of models whose features propagate to the next generation is based upon an objective function inspired by the Elo rating scheme, typically used to rate competitors in games such as chess and football. In all instances, our protocol finds models that exhibit $F_1$-score $\geq 0.88$ when compared with the true model, and it precisely identifies the true model in 72% of cases, whilst exploring a space of over $250,000$ potential models. By testing which interactions actually occur in the target system, QMLA is a viable tool for both the exploration of fundamental physics and the characterisation and calibration of quantum devices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge