Let Quantum Neural Networks Choose Their Own Frequencies

Parameterized quantum circuits as machine learning models are typically well described by their representation as a partial Fourier series of the input features, with frequencies uniquely determined by the feature map's generator Hamiltonians. Ordinarily, these data-encoding generators are chosen in advance, fixing the space of functions that can be represented. In this work we consider a generalization of quantum models to include a set of trainable parameters in the generator, leading to a trainable frequency (TF) quantum model. We numerically demonstrate how TF models can learn generators with desirable properties for solving the task at hand, including non-regularly spaced frequencies in their spectra and flexible spectral richness. Finally, we showcase the real-world effectiveness of our approach, demonstrating an improved accuracy in solving the Navier-Stokes equations using a TF model with only a single parameter added to each encoding operation. Since TF models encompass conventional fixed frequency models, they may offer a sensible default choice for variational quantum machine learning.

Harmonic (Quantum) Neural Networks

Harmonic functions are abundant in nature, appearing in limiting cases of Maxwell's, Navier-Stokes equations, the heat and the wave equation. Consequently, there are many applications of harmonic functions, spanning applications from industrial process optimisation to robotic path planning and the calculation of first exit times of random walks. Despite their ubiquity and relevance, there have been few attempts to develop effective means of representing harmonic functions in the context of machine learning architectures, either in machine learning on classical computers, or in the nascent field of quantum machine learning. Architectures which impose or encourage an inductive bias towards harmonic functions would facilitate data-driven modelling and the solution of inverse problems in a range of applications. For classical neural networks, it has already been established how leveraging inductive biases can in general lead to improved performance of learning algorithms. The introduction of such inductive biases within a quantum machine learning setting is instead still in its nascent stages. In this work, we derive exactly-harmonic (conventional- and quantum-) neural networks in two dimensions for simply-connected domains by leveraging the characteristics of holomorphic complex functions. We then demonstrate how these can be approximately extended to multiply-connected two-dimensional domains using techniques inspired by domain decomposition in physics-informed neural networks. We further provide architectures and training protocols to effectively impose approximately harmonic constraints in three dimensions and higher, and as a corollary we report divergence-free network architectures in arbitrary dimensions. Our approaches are demonstrated with applications to heat transfer, electrostatics and robot navigation, with comparisons to physics-informed neural networks included.

Learning models of quantum systems from experiments

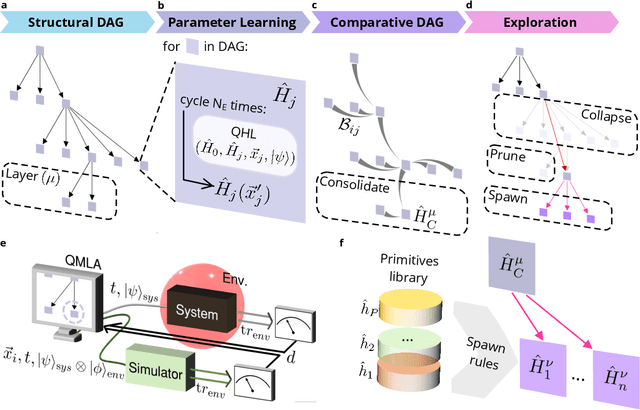
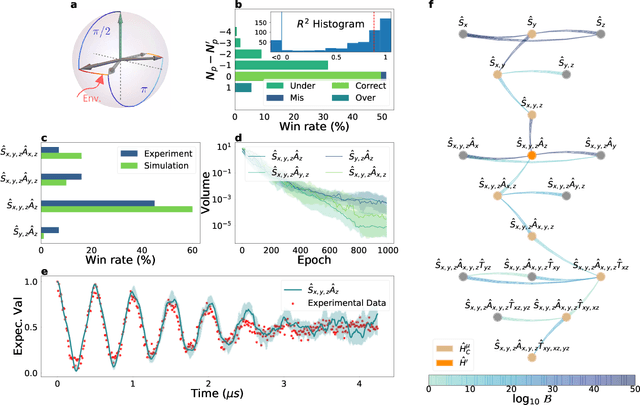
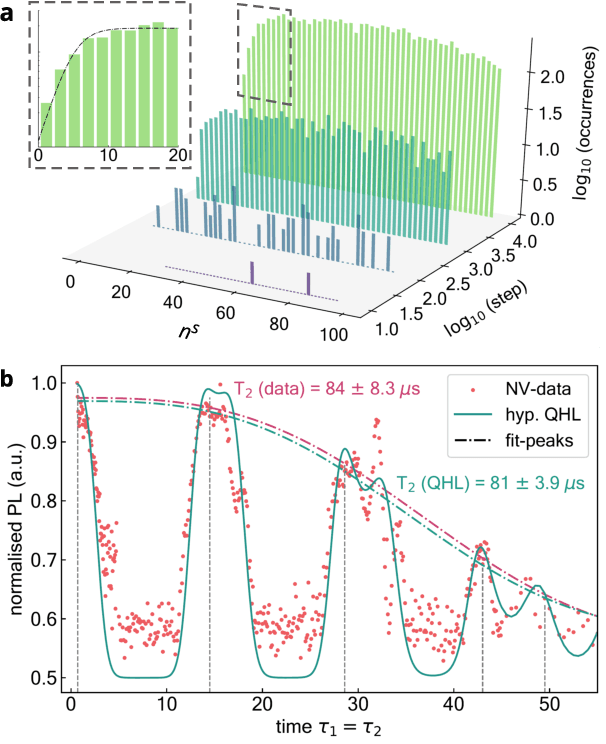
An isolated system of interacting quantum particles is described by a Hamiltonian operator. Hamiltonian models underpin the study and analysis of physical and chemical processes throughout science and industry, so it is crucial they are faithful to the system they represent. However, formulating and testing Hamiltonian models of quantum systems from experimental data is difficult because it is impossible to directly observe which interactions the quantum system is subject to. Here, we propose and demonstrate an approach to retrieving a Hamiltonian model from experiments, using unsupervised machine learning. We test our methods experimentally on an electron spin in a nitrogen-vacancy interacting with its spin bath environment, and numerically, finding success rates up to 86%. By building agents capable of learning science, which recover meaningful representations, we can gain further insight on the physics of quantum systems.