Atiyo Ghosh
Harmonic (Quantum) Neural Networks
Dec 14, 2022Abstract:Harmonic functions are abundant in nature, appearing in limiting cases of Maxwell's, Navier-Stokes equations, the heat and the wave equation. Consequently, there are many applications of harmonic functions, spanning applications from industrial process optimisation to robotic path planning and the calculation of first exit times of random walks. Despite their ubiquity and relevance, there have been few attempts to develop effective means of representing harmonic functions in the context of machine learning architectures, either in machine learning on classical computers, or in the nascent field of quantum machine learning. Architectures which impose or encourage an inductive bias towards harmonic functions would facilitate data-driven modelling and the solution of inverse problems in a range of applications. For classical neural networks, it has already been established how leveraging inductive biases can in general lead to improved performance of learning algorithms. The introduction of such inductive biases within a quantum machine learning setting is instead still in its nascent stages. In this work, we derive exactly-harmonic (conventional- and quantum-) neural networks in two dimensions for simply-connected domains by leveraging the characteristics of holomorphic complex functions. We then demonstrate how these can be approximately extended to multiply-connected two-dimensional domains using techniques inspired by domain decomposition in physics-informed neural networks. We further provide architectures and training protocols to effectively impose approximately harmonic constraints in three dimensions and higher, and as a corollary we report divergence-free network architectures in arbitrary dimensions. Our approaches are demonstrated with applications to heat transfer, electrostatics and robot navigation, with comparisons to physics-informed neural networks included.
Quantum Model-Discovery
Nov 11, 2021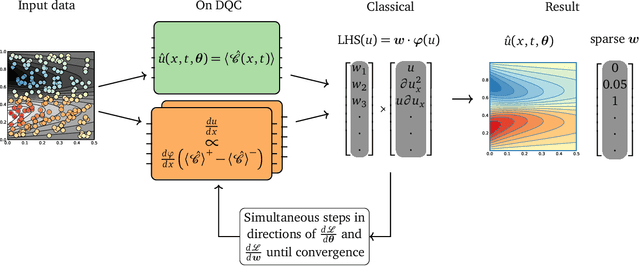

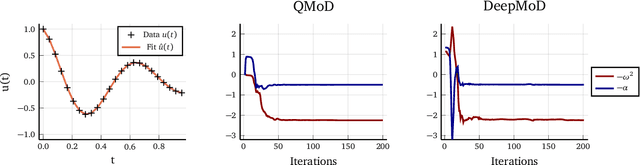

Abstract:Quantum computing promises to speed up some of the most challenging problems in science and engineering. Quantum algorithms have been proposed showing theoretical advantages in applications ranging from chemistry to logistics optimization. Many problems appearing in science and engineering can be rewritten as a set of differential equations. Quantum algorithms for solving differential equations have shown a provable advantage in the fault-tolerant quantum computing regime, where deep and wide quantum circuits can be used to solve large linear systems like partial differential equations (PDEs) efficiently. Recently, variational approaches to solving non-linear PDEs also with near-term quantum devices were proposed. One of the most promising general approaches is based on recent developments in the field of scientific machine learning for solving PDEs. We extend the applicability of near-term quantum computers to more general scientific machine learning tasks, including the discovery of differential equations from a dataset of measurements. We use differentiable quantum circuits (DQCs) to solve equations parameterized by a library of operators, and perform regression on a combination of data and equations. Our results show a promising path to Quantum Model Discovery (QMoD), on the interface between classical and quantum machine learning approaches. We demonstrate successful parameter inference and equation discovery using QMoD on different systems including a second-order, ordinary differential equation and a non-linear, partial differential equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge