Qadence: a differentiable interface for digital-analog programs

Digital-analog quantum computing (DAQC) is an alternative paradigm for universal quantum computation combining digital single-qubit gates with global analog operations acting on a register of interacting qubits. Currently, no available open-source software is tailored to express, differentiate, and execute programs within the DAQC paradigm. In this work, we address this shortfall by presenting Qadence, a high-level programming interface for building complex digital-analog quantum programs developed at Pasqal. Thanks to its flexible interface, native differentiability, and focus on real-device execution, Qadence aims at advancing research on variational quantum algorithms built for native DAQC platforms such as Rydberg atom arrays.

Quantum Model-Discovery

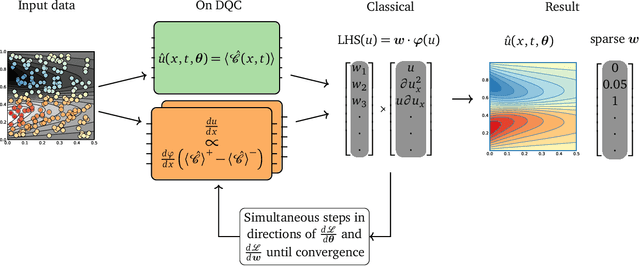
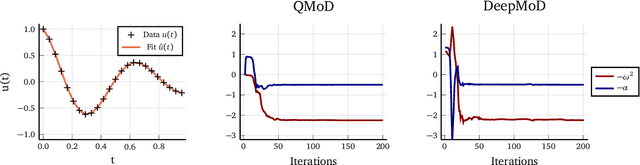
Quantum computing promises to speed up some of the most challenging problems in science and engineering. Quantum algorithms have been proposed showing theoretical advantages in applications ranging from chemistry to logistics optimization. Many problems appearing in science and engineering can be rewritten as a set of differential equations. Quantum algorithms for solving differential equations have shown a provable advantage in the fault-tolerant quantum computing regime, where deep and wide quantum circuits can be used to solve large linear systems like partial differential equations (PDEs) efficiently. Recently, variational approaches to solving non-linear PDEs also with near-term quantum devices were proposed. One of the most promising general approaches is based on recent developments in the field of scientific machine learning for solving PDEs. We extend the applicability of near-term quantum computers to more general scientific machine learning tasks, including the discovery of differential equations from a dataset of measurements. We use differentiable quantum circuits (DQCs) to solve equations parameterized by a library of operators, and perform regression on a combination of data and equations. Our results show a promising path to Quantum Model Discovery (QMoD), on the interface between classical and quantum machine learning approaches. We demonstrate successful parameter inference and equation discovery using QMoD on different systems including a second-order, ordinary differential equation and a non-linear, partial differential equation.

Neural Power Units

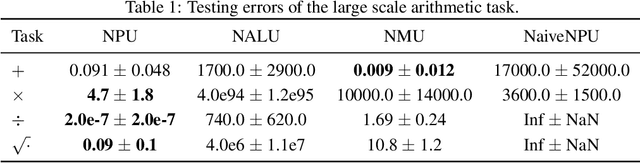
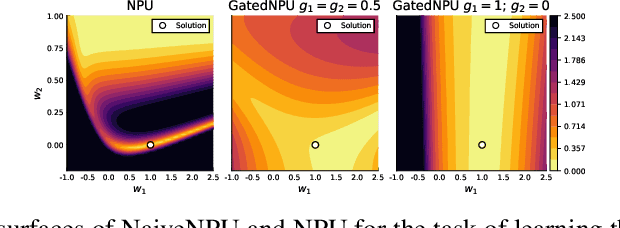
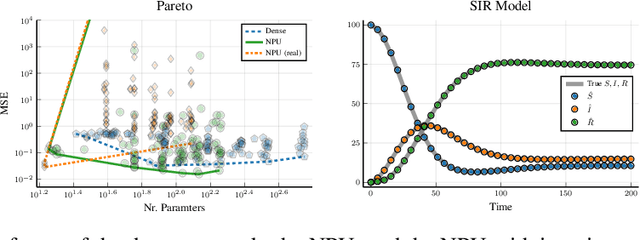
Conventional Neural Networks can approximate simple arithmetic operations, but fail to generalize beyond the range of numbers that were seen during training. Neural Arithmetic Units aim to overcome this difficulty, but current arithmetic units are either limited to operate on positive numbers or can only represent a subset of arithmetic operations. We introduce the Neural Power Unit (NPU) that operates on the full domain of real numbers and is capable of learning arbitrary power functions in a single layer. The NPU thus fixes the shortcomings of existing arithmetic units and extends their expressivity. We achieve this by using complex arithmetic without requiring a conversion of the network to complex numbers. A simplification of the unit to the RealNPU yields a highly interpretable model. We show that the NPUs outperform their competitors in terms of accuracy and sparsity on artificial arithmetic datasets, and that the RealNPU can discover the governing equations of a dynamical systems only from data.

Rodent: Relevance determination in ODE

From a set of observed trajectories of a partially observed system, we aim to learn its underlying (physical) process without having to make too many assumptions about the generating model. We start with a very general, over-parameterized ordinary differential equation (ODE) of order N and learn the minimal complexity of the model, by which we mean both the order of the ODE as well as the minimum number of non-zero parameters that are needed to solve the problem. The minimal complexity is found by combining the Variational Auto-Encoder (VAE) with Automatic Relevance Determination (ARD) to the problem of learning the parameters of an ODE which we call Rodent. We show that it is possible to learn not only one specific model for a single process, but a manifold of models representing harmonic signals in general.

Adaptive Anomaly Detection in Chaotic Time Series with a Spatially Aware Echo State Network

This work builds an automated anomaly detection method for chaotic time series, and more concretely for turbulent, high-dimensional, ocean simulations. We solve this task by extending the Echo State Network by spatially aware input maps, such as convolutions, gradients, cosine transforms, et cetera, as well as a spatially aware loss function. The spatial ESN is used to create predictions which reduce the detection problem to thresholding of the prediction error. We benchmark our detection framework on different tasks of increasing difficulty to show the generality of the framework before applying it to raw climate model output in the region of the Japanese ocean current Kuroshio, which exhibits a bimodality that is not easily detected by the naked eye. The code is available as an open source Python package, Torsk, available at https://github.com/nmheim/torsk, where we also provide supplementary material and programs that reproduce the results shown in this paper.