Qadence: a differentiable interface for digital-analog programs

Digital-analog quantum computing (DAQC) is an alternative paradigm for universal quantum computation combining digital single-qubit gates with global analog operations acting on a register of interacting qubits. Currently, no available open-source software is tailored to express, differentiate, and execute programs within the DAQC paradigm. In this work, we address this shortfall by presenting Qadence, a high-level programming interface for building complex digital-analog quantum programs developed at Pasqal. Thanks to its flexible interface, native differentiability, and focus on real-device execution, Qadence aims at advancing research on variational quantum algorithms built for native DAQC platforms such as Rydberg atom arrays.

Discovering PDEs from Multiple Experiments

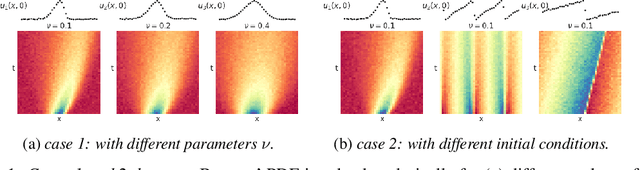
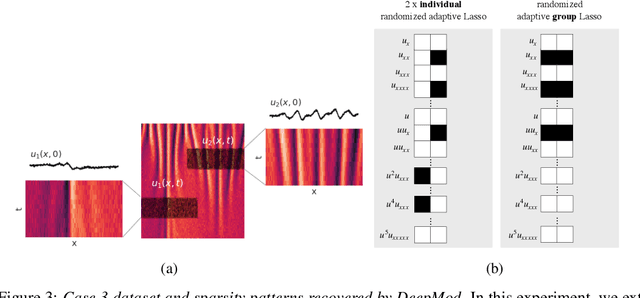
Automated model discovery of partial differential equations (PDEs) usually considers a single experiment or dataset to infer the underlying governing equations. In practice, experiments have inherent natural variability in parameters, initial and boundary conditions that cannot be simply averaged out. We introduce a randomised adaptive group Lasso sparsity estimator to promote grouped sparsity and implement it in a deep learning based PDE discovery framework. It allows to create a learning bias that implies the a priori assumption that all experiments can be explained by the same underlying PDE terms with potentially different coefficients. Our experimental results show more generalizable PDEs can be found from multiple highly noisy datasets, by this grouped sparsity promotion rather than simply performing independent model discoveries.

Sparsistent Model Discovery

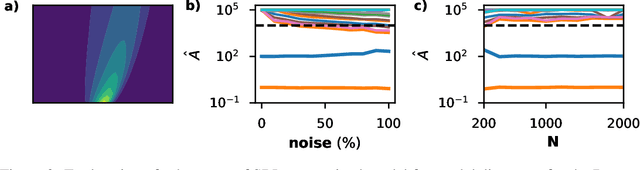
Discovering the partial differential equations underlying a spatio-temporal datasets from very limited observations is of paramount interest in many scientific fields. However, it remains an open question to know when model discovery algorithms based on sparse regression can actually recover the underlying physical processes. We trace back the poor of performance of Lasso based model discovery algorithms to its potential variable selection inconsistency: meaning that even if the true model is present in the library, it might not be selected. By first revisiting the irrepresentability condition (IRC) of the Lasso, we gain some insights of when this might occur. We then show that the adaptive Lasso will have more chances of verifying the IRC than the Lasso and propose to integrate it within a deep learning model discovery framework with stability selection and error control. Experimental results show we can recover several nonlinear and chaotic canonical PDEs with a single set of hyperparameters from a very limited number of samples at high noise levels.

Fully differentiable model discovery

Model discovery aims at autonomously discovering differential equations underlying a dataset. Approaches based on Physics Informed Neural Networks (PINNs) have shown great promise, but a fully-differentiable model which explicitly learns the equation has remained elusive. In this paper we propose such an approach by combining neural network based surrogates with Sparse Bayesian Learning (SBL). We start by reinterpreting PINNs as multitask models, applying multitask learning using uncertainty, and show that this leads to a natural framework for including Bayesian regression techniques. We then construct a robust model discovery algorithm by using SBL, which we showcase on various datasets. Concurrently, the multitask approach allows the use of probabilistic approximators, and we show a proof of concept using normalizing flows to directly learn a density model from single particle data. Our work expands PINNs to various types of neural network architectures, and connects neural network-based surrogates to the rich field of Bayesian parameter inference.

Model discovery in the sparse sampling regime

To improve the physical understanding and the predictions of complex dynamic systems, such as ocean dynamics and weather predictions, it is of paramount interest to identify interpretable models from coarsely and off-grid sampled observations. In this work, we investigate how deep learning can improve model discovery of partial differential equations when the spacing between sensors is large and the samples are not placed on a grid. We show how leveraging physics informed neural network interpolation and automatic differentiation, allow to better fit the data and its spatiotemporal derivatives, compared to more classic spline interpolation and numerical differentiation techniques. As a result, deep learning-based model discovery allows to recover the underlying equations, even when sensors are placed further apart than the data's characteristic length scale and in the presence of high noise levels. We illustrate our claims on both synthetic and experimental data sets where combinations of physical processes such as (non)-linear advection, reaction, and diffusion are correctly identified.

Sparsely constrained neural networks for model discovery of PDEs

Sparse regression on a library of candidate features has developed as the prime method to discover the PDE underlying a spatio-temporal dataset. As these features consist of higher order derivatives, model discovery is typically limited to low-noise and dense datasets due to the erros inherent to numerical differentiation. Neural network-based approaches circumvent this limit, but to date have ignored advances in sparse regression algorithms. In this paper we present a modular framework that combines deep-learning based approaches with an arbitrary sparse regression technique. We demonstrate with several examples that this combination facilitates and enhances model discovery tasks. We release our framework as a package at https://github.com/PhIMaL/DeePyMoD

Temporal Normalizing Flows

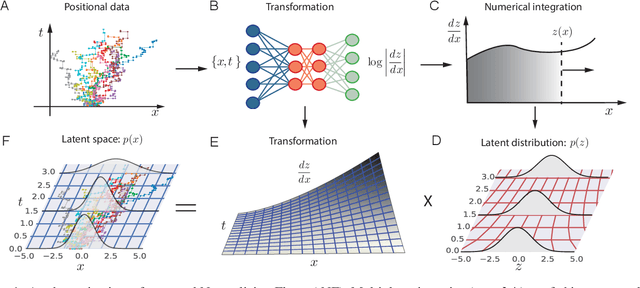
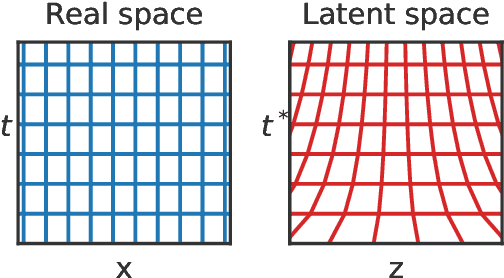
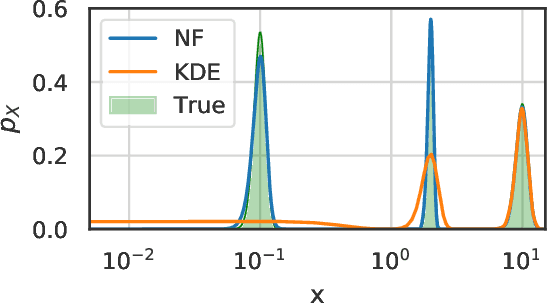
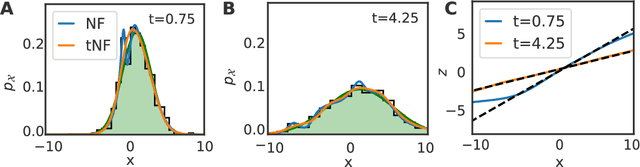
Analyzing and interpreting time-dependent stochastic data requires accurate and robust density estimation. In this paper we extend the concept of normalizing flows to so-called temporal Normalizing Flows (tNFs) to estimate time dependent distributions, leveraging the full spatio-temporal information present in the dataset. Our approach is unsupervised, does not require an a-priori characteristic scale and can accurately estimate multi-scale distributions of vastly different length scales. We illustrate tNFs on sparse datasets of Brownian and chemotactic walkers, showing that the inclusion of temporal information enhances density estimation. Finally, we speculate how tNFs can be applied to fit and discover the continuous PDE underlying a stochastic process.

DeepMoD: Deep learning for Model Discovery in noisy data

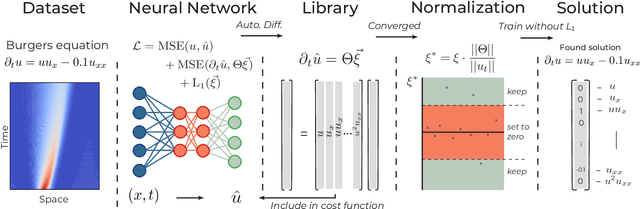
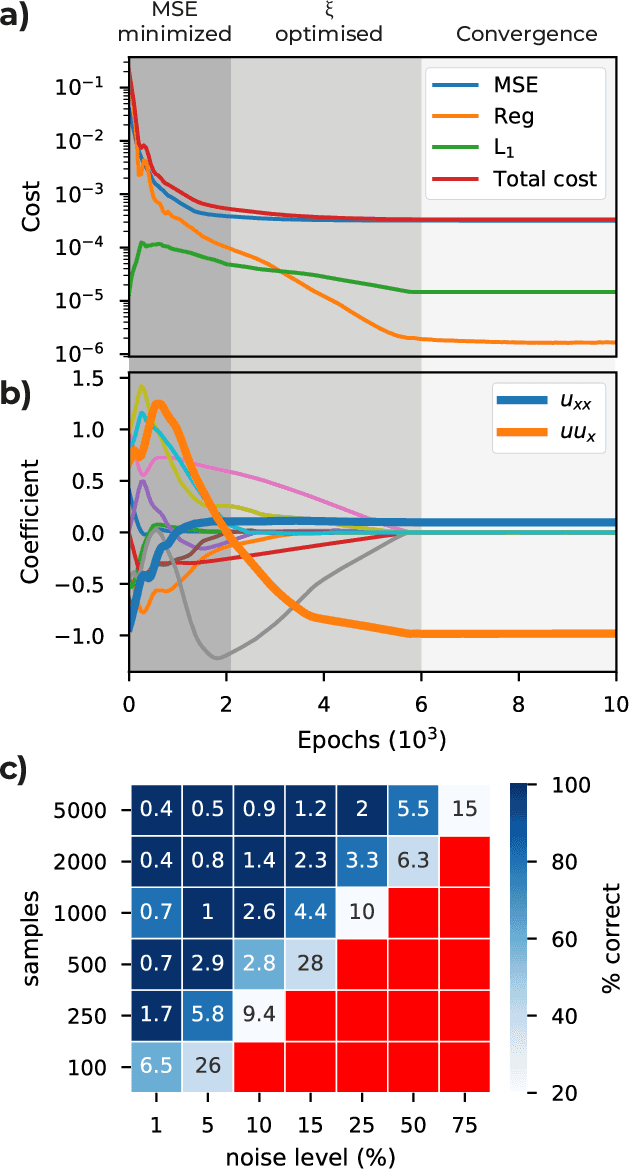
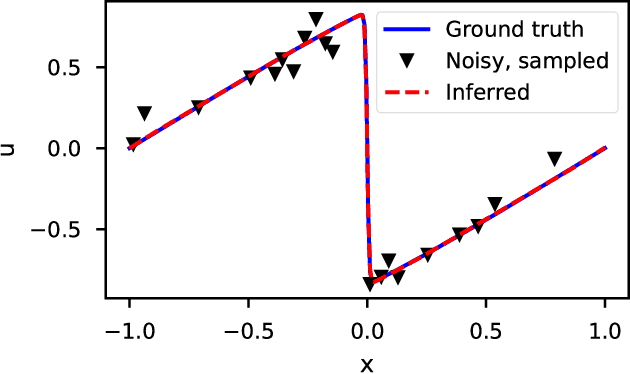
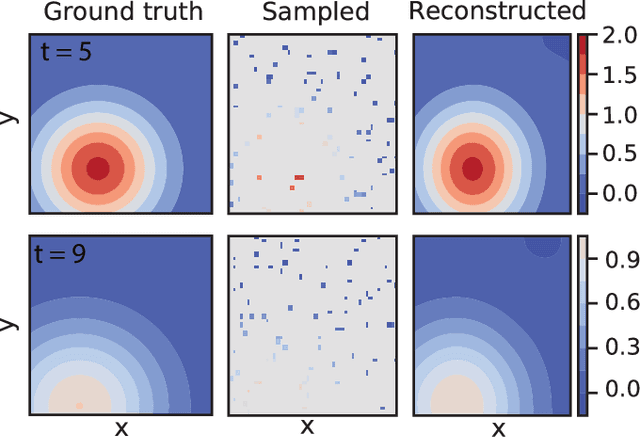
We introduce DeepMoD, a deep learning based model discovery algorithm which seeks the partial differential equation underlying a spatio-temporal data set. DeepMoD employs sparse regression on a library of basis functions and their corresponding spatial derivatives. A feed-forward neural network approximates the data set and automatic differentiation is used to construct this function library and perform regression within the neural network. This construction makes it extremely robust to noise and applicable to small data sets and, contrary to other deep learning methods, does not require a training set and is impervious to overfitting. We illustrate this approach on several physical problems, such as the Burgers', Korteweg-de Vries, advection-diffusion and Keller-Segel equations, and find that it requires as few as O(10^2) samples and works at noise levels up to 75%. This resilience to noise and high performance at very few samples highlights the potential of this method to be applied on experimental data. Code and examples available at https://github.com/PhIMaL/DeePyMoD.