Augmenting train maintenance technicians with automated incident diagnostic suggestions

Train operational incidents are so far diagnosed individually and manually by train maintenance technicians. In order to assist maintenance crews in their responsiveness and task prioritization, a learning machine is developed and deployed in production to suggest diagnostics to train technicians on their phones, tablets or laptops as soon as a train incident is declared. A feedback loop allows to take into account the actual diagnose by designated train maintenance experts to refine the learning machine. By formulating the problem as a discrete set classification task, feature engineering methods are proposed to extract physically plausible sets of events from traces generated on-board railway vehicles. The latter feed an original ensemble classifier to class incidents by their potential technical cause. Finally, the resulting model is trained and validated using real operational data and deployed on a cloud platform. Future work will explore how the extracted sets of events can be used to avoid incidents by assisting human experts in the creation predictive maintenance alerts.

Discovering PDEs from Multiple Experiments

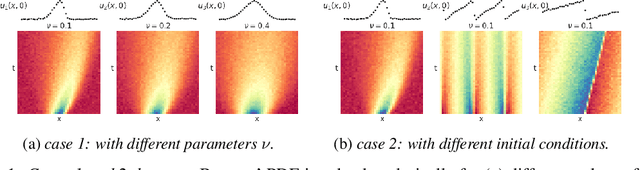
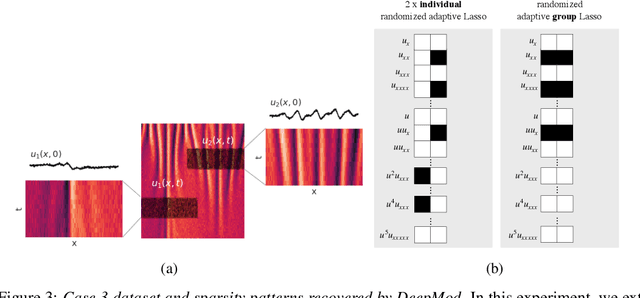
Automated model discovery of partial differential equations (PDEs) usually considers a single experiment or dataset to infer the underlying governing equations. In practice, experiments have inherent natural variability in parameters, initial and boundary conditions that cannot be simply averaged out. We introduce a randomised adaptive group Lasso sparsity estimator to promote grouped sparsity and implement it in a deep learning based PDE discovery framework. It allows to create a learning bias that implies the a priori assumption that all experiments can be explained by the same underlying PDE terms with potentially different coefficients. Our experimental results show more generalizable PDEs can be found from multiple highly noisy datasets, by this grouped sparsity promotion rather than simply performing independent model discoveries.

Sparsistent Model Discovery

Discovering the partial differential equations underlying a spatio-temporal datasets from very limited observations is of paramount interest in many scientific fields. However, it remains an open question to know when model discovery algorithms based on sparse regression can actually recover the underlying physical processes. We trace back the poor of performance of Lasso based model discovery algorithms to its potential variable selection inconsistency: meaning that even if the true model is present in the library, it might not be selected. By first revisiting the irrepresentability condition (IRC) of the Lasso, we gain some insights of when this might occur. We then show that the adaptive Lasso will have more chances of verifying the IRC than the Lasso and propose to integrate it within a deep learning model discovery framework with stability selection and error control. Experimental results show we can recover several nonlinear and chaotic canonical PDEs with a single set of hyperparameters from a very limited number of samples at high noise levels.

Model discovery in the sparse sampling regime

To improve the physical understanding and the predictions of complex dynamic systems, such as ocean dynamics and weather predictions, it is of paramount interest to identify interpretable models from coarsely and off-grid sampled observations. In this work, we investigate how deep learning can improve model discovery of partial differential equations when the spacing between sensors is large and the samples are not placed on a grid. We show how leveraging physics informed neural network interpolation and automatic differentiation, allow to better fit the data and its spatiotemporal derivatives, compared to more classic spline interpolation and numerical differentiation techniques. As a result, deep learning-based model discovery allows to recover the underlying equations, even when sensors are placed further apart than the data's characteristic length scale and in the presence of high noise levels. We illustrate our claims on both synthetic and experimental data sets where combinations of physical processes such as (non)-linear advection, reaction, and diffusion are correctly identified.