DeepMoD: Deep learning for Model Discovery in noisy data

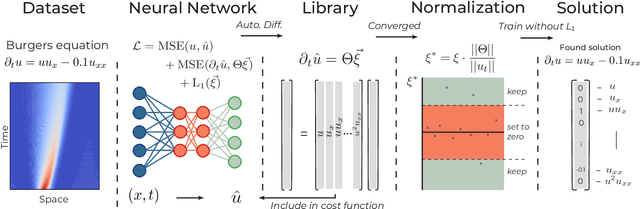
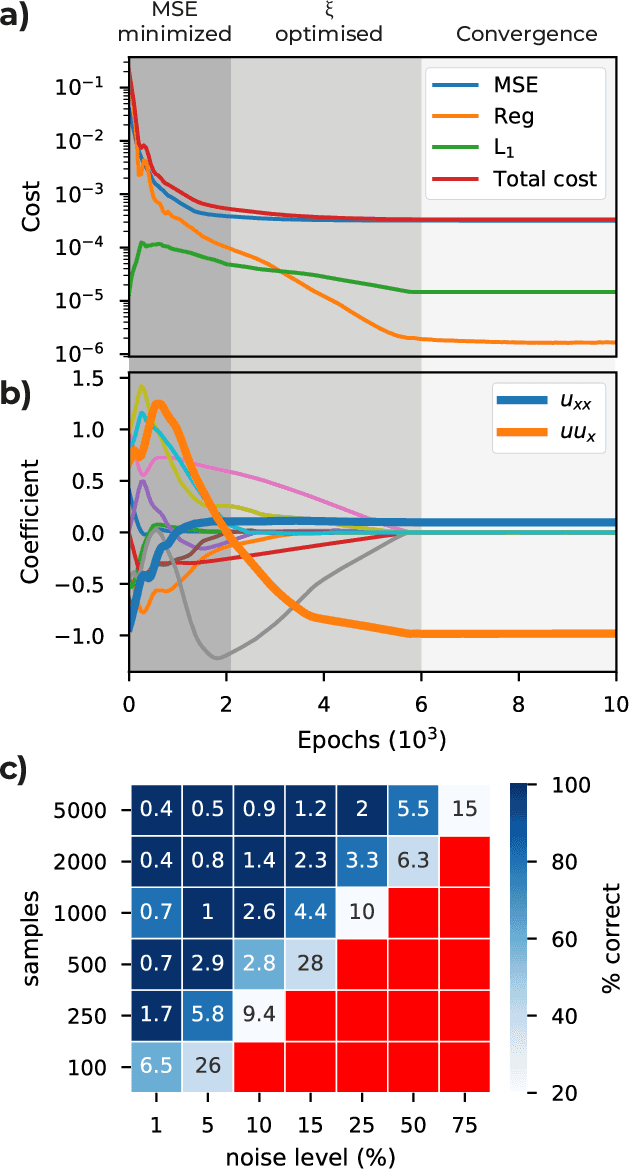
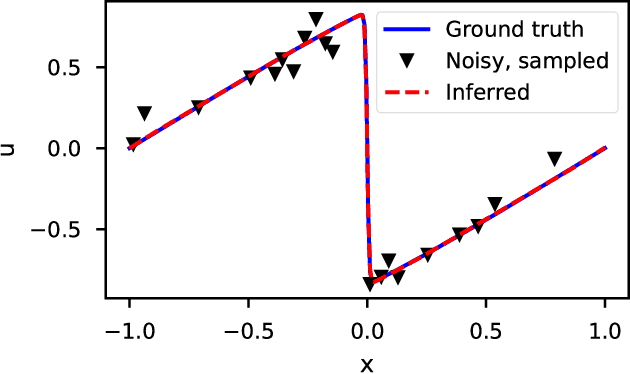
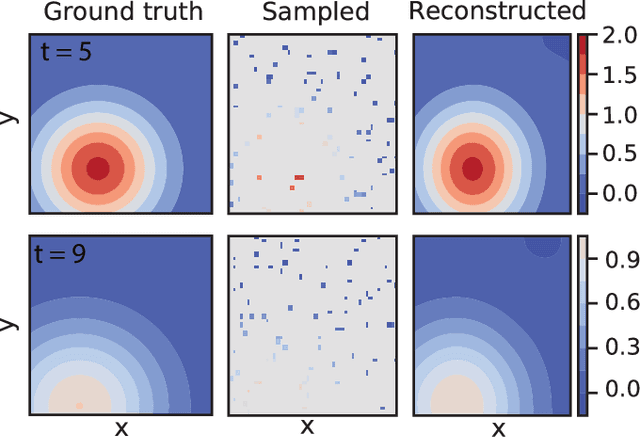
We introduce DeepMoD, a deep learning based model discovery algorithm which seeks the partial differential equation underlying a spatio-temporal data set. DeepMoD employs sparse regression on a library of basis functions and their corresponding spatial derivatives. A feed-forward neural network approximates the data set and automatic differentiation is used to construct this function library and perform regression within the neural network. This construction makes it extremely robust to noise and applicable to small data sets and, contrary to other deep learning methods, does not require a training set and is impervious to overfitting. We illustrate this approach on several physical problems, such as the Burgers', Korteweg-de Vries, advection-diffusion and Keller-Segel equations, and find that it requires as few as O(10^2) samples and works at noise levels up to 75%. This resilience to noise and high performance at very few samples highlights the potential of this method to be applied on experimental data. Code and examples available at https://github.com/PhIMaL/DeePyMoD.