A unifying framework for relaxations of the causal assumptions in Bell's theorem
Paper and Code
Nov 17, 2014

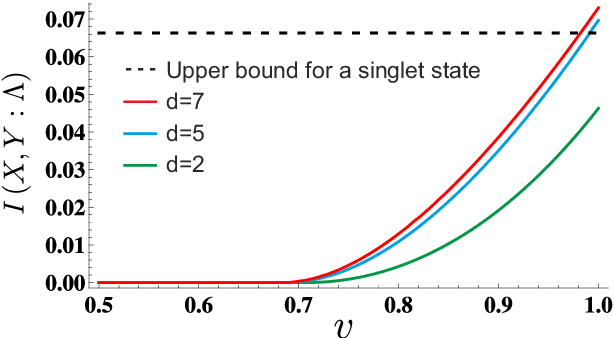
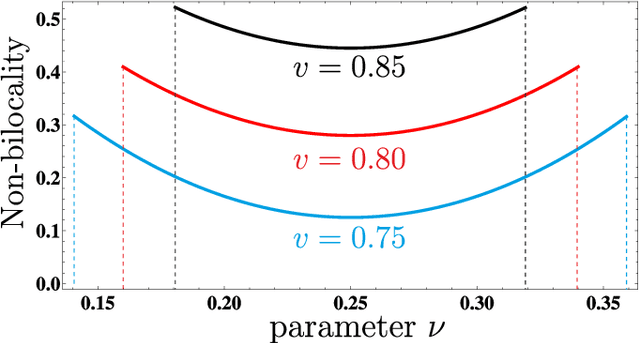
Bell's Theorem shows that quantum mechanical correlations can violate the constraints that the causal structure of certain experiments impose on any classical explanation. It is thus natural to ask to which degree the causal assumptions -- e.g. locality or measurement independence -- have to be relaxed in order to allow for a classical description of such experiments. Here, we develop a conceptual and computational framework for treating this problem. We employ the language of Bayesian networks to systematically construct alternative causal structures and bound the degree of relaxation using quantitative measures that originate from the mathematical theory of causality. The main technical insight is that the resulting problems can often be expressed as computationally tractable linear programs. We demonstrate the versatility of the framework by applying it to a variety of scenarios, ranging from relaxations of the measurement independence, locality and bilocality assumptions, to a novel causal interpretation of CHSH inequality violations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge