Proof methods for robust low-rank matrix recovery

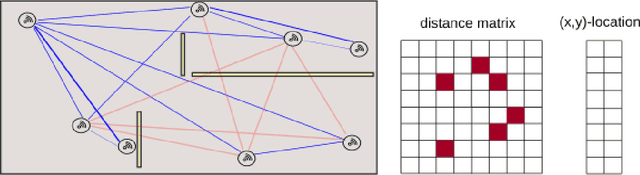
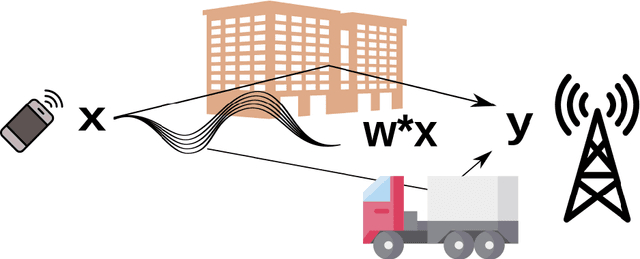
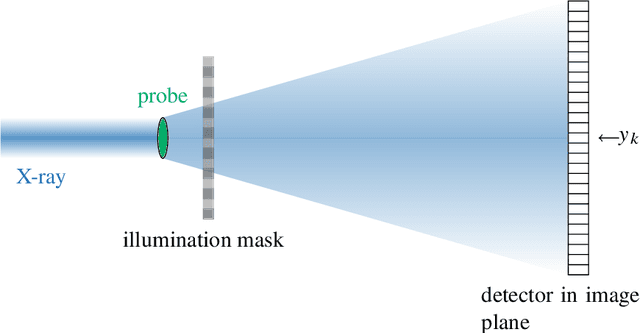
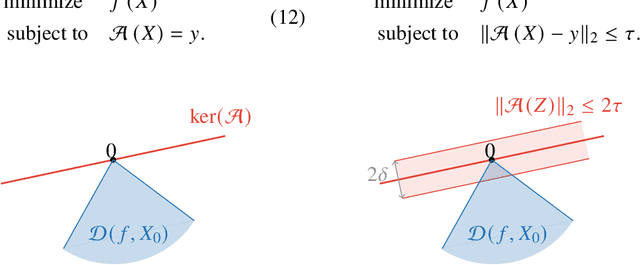
Low-rank matrix recovery problems arise naturally as mathematical formulations of various inverse problems, such as matrix completion, blind deconvolution, and phase retrieval. Over the last two decades, a number of works have rigorously analyzed the reconstruction performance for such scenarios, giving rise to a rather general understanding of the potential and the limitations of low-rank matrix models in sensing problems. In this article, we compare the two main proof techniques that have been paving the way to a rigorous analysis, discuss their potential and limitations, and survey their successful applications. On the one hand, we review approaches based on descent cone analysis, showing that they often lead to strong guarantees even in the presence of adversarial noise, but face limitations when it comes to structured observations. On the other hand, we discuss techniques using approximate dual certificates and the golfing scheme, which are often better suited to deal with practical measurement structures, but sometimes lead to weaker guarantees. Lastly, we review recent progress towards analyzing descent cones also for structured scenarios -- exploiting the idea of splitting the cones into multiple parts that are analyzed via different techniques.

Semidefinite tests for latent causal structures

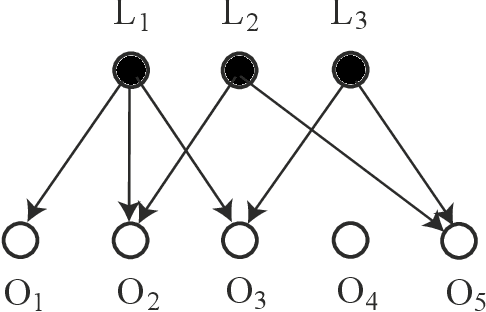
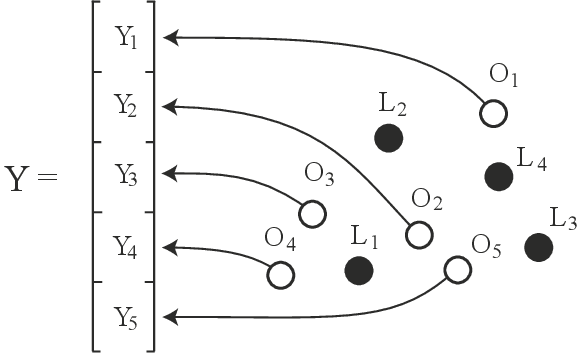
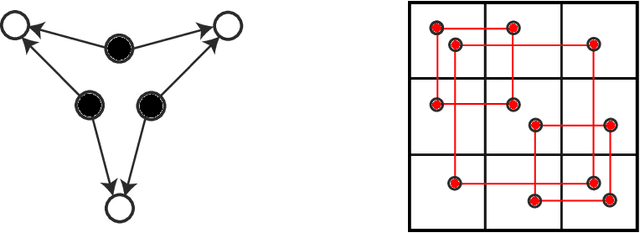
Testing whether a probability distribution is compatible with a given Bayesian network is a fundamental task in the field of causal inference, where Bayesian networks model causal relations. Here we consider the class of causal structures where all correlations between observed quantities are solely due to the influence from latent variables. We show that each model of this type imposes a certain signature on the observable covariance matrix in terms of a particular decomposition into positive semidefinite components. This signature, and thus the underlying hypothetical latent structure, can be tested in a computationally efficient manner via semidefinite programming. This stands in stark contrast with the algebraic geometric tools required if the full observable probability distribution is taken into account. The semidefinite test is compared with tests based on entropic inequalities.

A unifying framework for relaxations of the causal assumptions in Bell's theorem

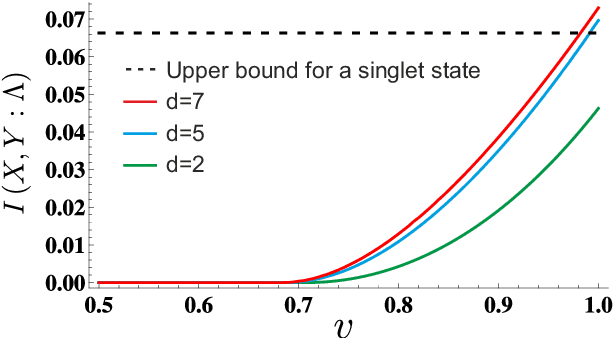
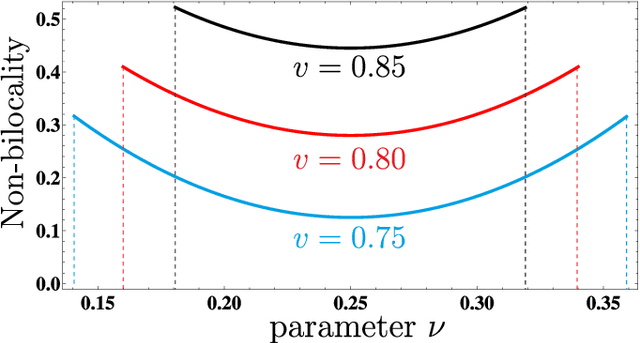
Bell's Theorem shows that quantum mechanical correlations can violate the constraints that the causal structure of certain experiments impose on any classical explanation. It is thus natural to ask to which degree the causal assumptions -- e.g. locality or measurement independence -- have to be relaxed in order to allow for a classical description of such experiments. Here, we develop a conceptual and computational framework for treating this problem. We employ the language of Bayesian networks to systematically construct alternative causal structures and bound the degree of relaxation using quantitative measures that originate from the mathematical theory of causality. The main technical insight is that the resulting problems can often be expressed as computationally tractable linear programs. We demonstrate the versatility of the framework by applying it to a variety of scenarios, ranging from relaxations of the measurement independence, locality and bilocality assumptions, to a novel causal interpretation of CHSH inequality violations.