Proof methods for robust low-rank matrix recovery
Paper and Code
Jun 08, 2021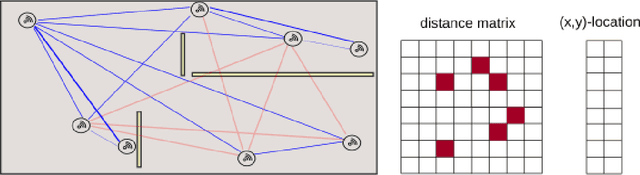
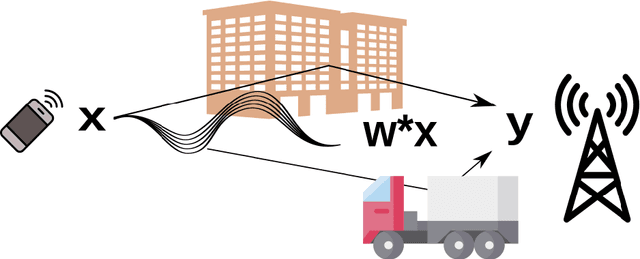
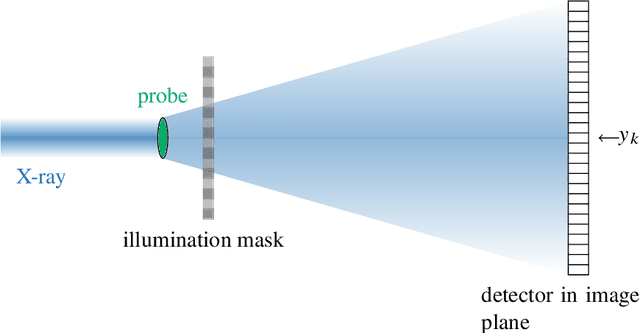
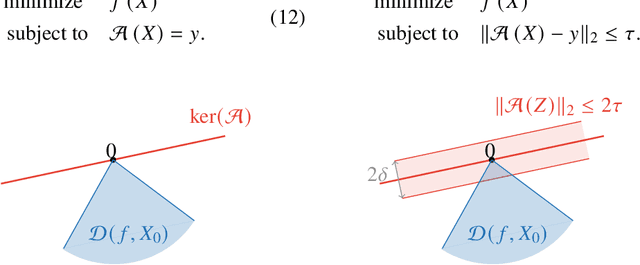
Low-rank matrix recovery problems arise naturally as mathematical formulations of various inverse problems, such as matrix completion, blind deconvolution, and phase retrieval. Over the last two decades, a number of works have rigorously analyzed the reconstruction performance for such scenarios, giving rise to a rather general understanding of the potential and the limitations of low-rank matrix models in sensing problems. In this article, we compare the two main proof techniques that have been paving the way to a rigorous analysis, discuss their potential and limitations, and survey their successful applications. On the one hand, we review approaches based on descent cone analysis, showing that they often lead to strong guarantees even in the presence of adversarial noise, but face limitations when it comes to structured observations. On the other hand, we discuss techniques using approximate dual certificates and the golfing scheme, which are often better suited to deal with practical measurement structures, but sometimes lead to weaker guarantees. Lastly, we review recent progress towards analyzing descent cones also for structured scenarios -- exploiting the idea of splitting the cones into multiple parts that are analyzed via different techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge