An Automated Approach to Causal Inference in Discrete Settings

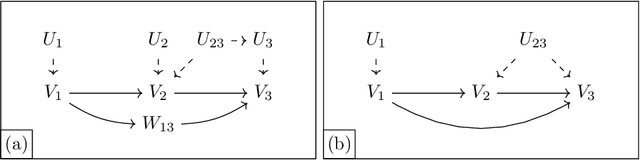
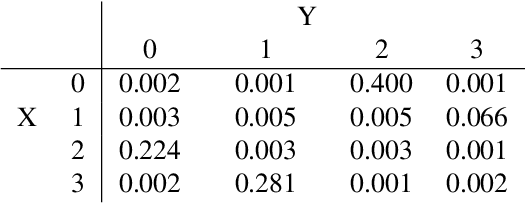
When causal quantities cannot be point identified, researchers often pursue partial identification to quantify the range of possible values. However, the peculiarities of applied research conditions can make this analytically intractable. We present a general and automated approach to causal inference in discrete settings. We show causal questions with discrete data reduce to polynomial programming problems, and we present an algorithm to automatically bound causal effects using efficient dual relaxation and spatial branch-and-bound techniques. The user declares an estimand, states assumptions, and provides data (however incomplete or mismeasured). The algorithm then searches over admissible data-generating processes and outputs the most precise possible range consistent with available information -- i.e., sharp bounds -- including a point-identified solution if one exists. Because this search can be computationally intensive, our procedure reports and continually refines non-sharp ranges that are guaranteed to contain the truth at all times, even when the algorithm is not run to completion. Moreover, it offers an additional guarantee we refer to as $\epsilon$-sharpness, characterizing the worst-case looseness of the incomplete bounds. Analytically validated simulations show the algorithm accommodates classic obstacles, including confounding, selection, measurement error, noncompliance, and nonresponse.

Entropic Inequality Constraints from $e$-separation Relations in Directed Acyclic Graphs with Hidden Variables

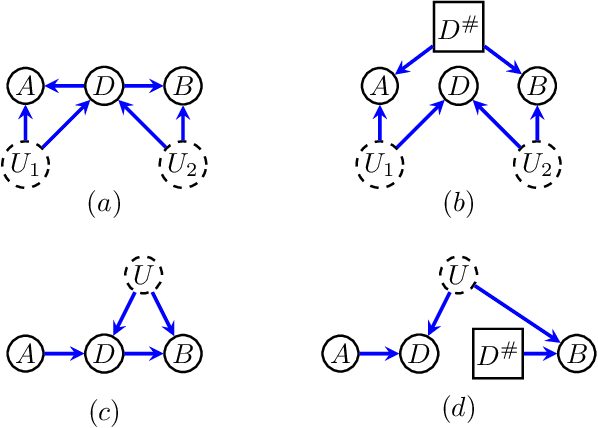
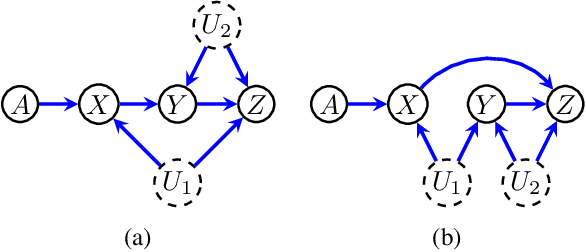
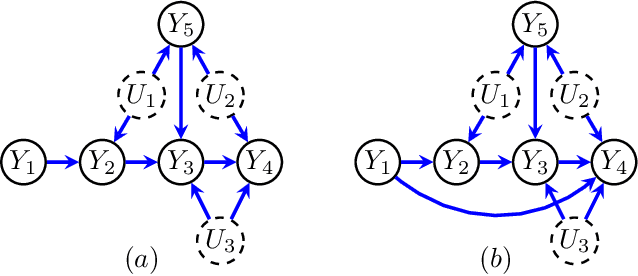
Directed acyclic graphs (DAGs) with hidden variables are often used to characterize causal relations between variables in a system. When some variables are unobserved, DAGs imply a notoriously complicated set of constraints on the distribution of observed variables. In this work, we present entropic inequality constraints that are implied by $e$-separation relations in hidden variable DAGs with discrete observed variables. The constraints can intuitively be understood to follow from the fact that the capacity of variables along a causal pathway to convey information is restricted by their entropy; e.g. at the extreme case, a variable with entropy $0$ can convey no information. We show how these constraints can be used to learn about the true causal model from an observed data distribution. In addition, we propose a measure of causal influence called the minimal mediary entropy, and demonstrate that it can augment traditional measures such as the average causal effect.

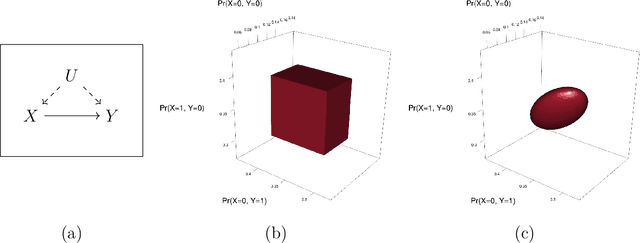
Partial Identifiability in Discrete Data With Measurement Error

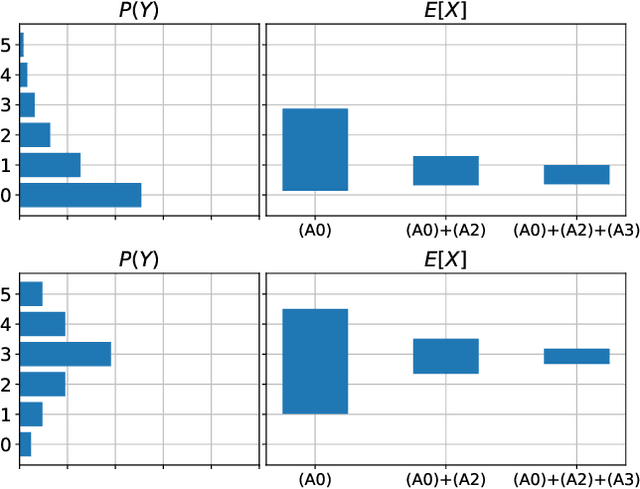
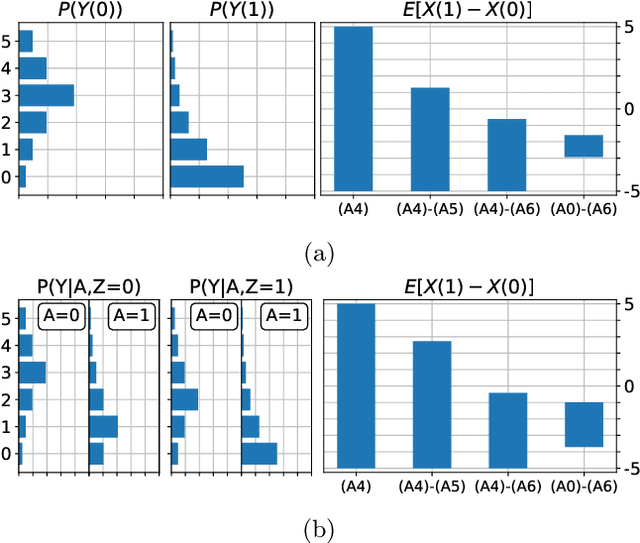
When data contains measurement errors, it is necessary to make assumptions relating the observed, erroneous data to the unobserved true phenomena of interest. These assumptions should be justifiable on substantive grounds, but are often motivated by mathematical convenience, for the sake of exactly identifying the target of inference. We adopt the view that it is preferable to present bounds under justifiable assumptions than to pursue exact identification under dubious ones. To that end, we demonstrate how a broad class of modeling assumptions involving discrete variables, including common measurement error and conditional independence assumptions, can be expressed as linear constraints on the parameters of the model. We then use linear programming techniques to produce sharp bounds for factual and counterfactual distributions under measurement error in such models. We additionally propose a procedure for obtaining outer bounds on non-linear models. Our method yields sharp bounds in a number of important settings -- such as the instrumental variable scenario with measurement error -- for which no bounds were previously known.

Deriving Bounds and Inequality Constraints Using LogicalRelations Among Counterfactuals

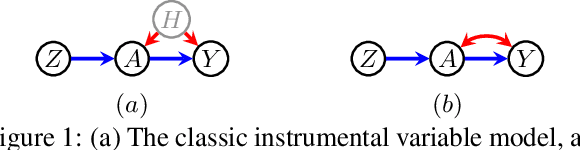
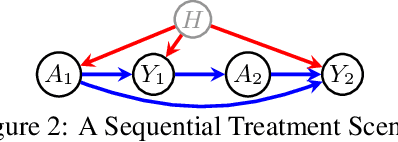
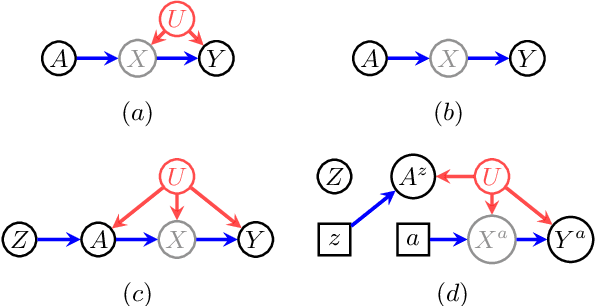
Causal parameters may not be point identified in the presence of unobserved confounding. However, information about non-identified parameters, in the form of bounds, may still be recovered from the observed data in some cases. We develop a new general method for obtaining bounds on causal parameters using rules of probability and restrictions on counterfactuals implied by causal graphical models. We additionally provide inequality constraints on functionals of the observed data law implied by such causal models. Our approach is motivated by the observation that logical relations between identified and non-identified counterfactual events often yield information about non-identified events. We show that this approach is powerful enough to recover known sharp bounds and tight inequality constraints, and to derive novel bounds and constraints.