Deriving Bounds and Inequality Constraints Using LogicalRelations Among Counterfactuals
Paper and Code
Jul 01, 2020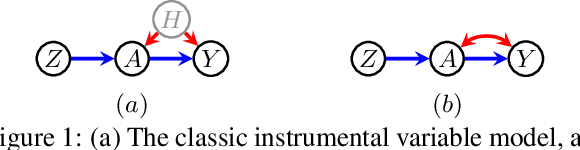
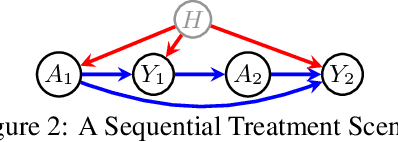


Causal parameters may not be point identified in the presence of unobserved confounding. However, information about non-identified parameters, in the form of bounds, may still be recovered from the observed data in some cases. We develop a new general method for obtaining bounds on causal parameters using rules of probability and restrictions on counterfactuals implied by causal graphical models. We additionally provide inequality constraints on functionals of the observed data law implied by such causal models. Our approach is motivated by the observation that logical relations between identified and non-identified counterfactual events often yield information about non-identified events. We show that this approach is powerful enough to recover known sharp bounds and tight inequality constraints, and to derive novel bounds and constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge