Identification of Single-Treatment Effects in Factorial Experiments

Despite their cost, randomized controlled trials (RCTs) are widely regarded as gold-standard evidence in disciplines ranging from social science to medicine. In recent decades, researchers have increasingly sought to reduce the resource burden of repeated RCTs with factorial designs that simultaneously test multiple hypotheses, e.g. experiments that evaluate the effects of many medications or products simultaneously. Here I show that when multiple interventions are randomized in experiments, the effect any single intervention would have outside the experimental setting is not identified absent heroic assumptions, even if otherwise perfectly realistic conditions are achieved. This happens because single-treatment effects involve a counterfactual world with a single focal intervention, allowing other variables to take their natural values (which may be confounded or modified by the focal intervention). In contrast, observational studies and factorial experiments provide information about potential-outcome distributions with zero and multiple interventions, respectively. In this paper, I formalize sufficient conditions for the identifiability of those isolated quantities. I show that researchers who rely on this type of design have to justify either linearity of functional forms or -- in the nonparametric case -- specify with Directed Acyclic Graphs how variables are related in the real world. Finally, I develop nonparametric sharp bounds -- i.e., maximally informative best-/worst-case estimates consistent with limited RCT data -- that show when extrapolations about effect signs are empirically justified. These new results are illustrated with simulated data.

An Automated Approach to Causal Inference in Discrete Settings

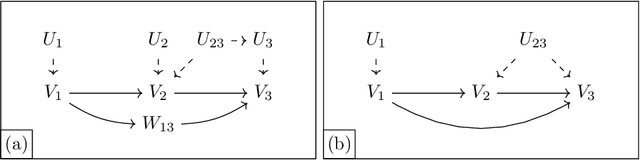
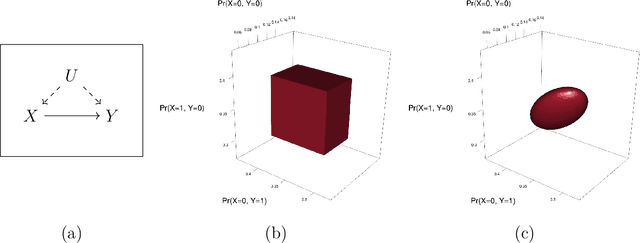
When causal quantities cannot be point identified, researchers often pursue partial identification to quantify the range of possible values. However, the peculiarities of applied research conditions can make this analytically intractable. We present a general and automated approach to causal inference in discrete settings. We show causal questions with discrete data reduce to polynomial programming problems, and we present an algorithm to automatically bound causal effects using efficient dual relaxation and spatial branch-and-bound techniques. The user declares an estimand, states assumptions, and provides data (however incomplete or mismeasured). The algorithm then searches over admissible data-generating processes and outputs the most precise possible range consistent with available information -- i.e., sharp bounds -- including a point-identified solution if one exists. Because this search can be computationally intensive, our procedure reports and continually refines non-sharp ranges that are guaranteed to contain the truth at all times, even when the algorithm is not run to completion. Moreover, it offers an additional guarantee we refer to as $\epsilon$-sharpness, characterizing the worst-case looseness of the incomplete bounds. Analytically validated simulations show the algorithm accommodates classic obstacles, including confounding, selection, measurement error, noncompliance, and nonresponse.