Partial Identifiability in Discrete Data With Measurement Error

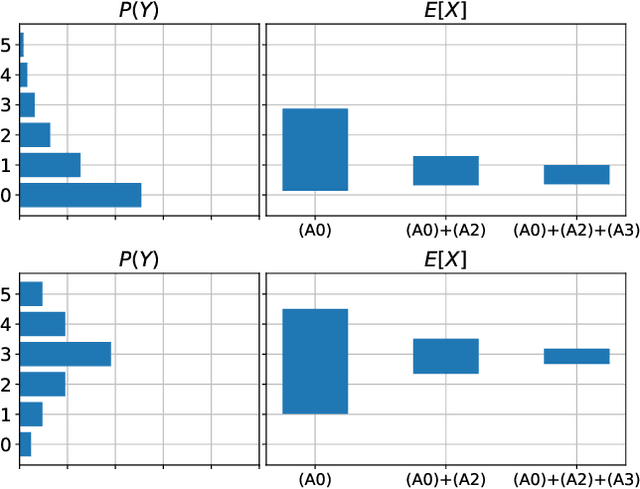
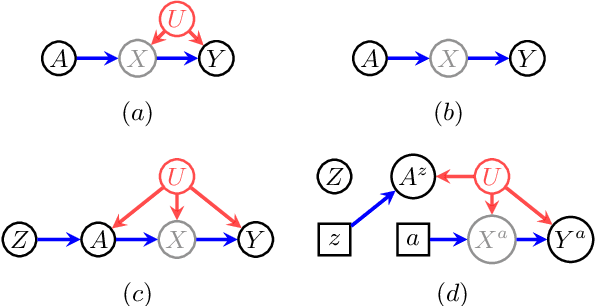
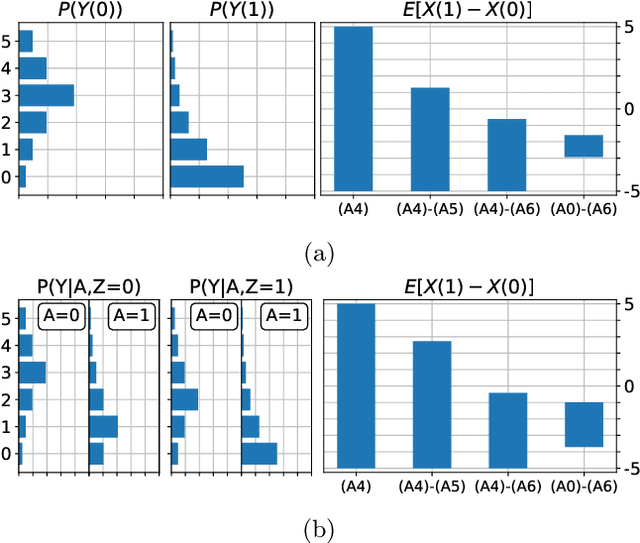
When data contains measurement errors, it is necessary to make assumptions relating the observed, erroneous data to the unobserved true phenomena of interest. These assumptions should be justifiable on substantive grounds, but are often motivated by mathematical convenience, for the sake of exactly identifying the target of inference. We adopt the view that it is preferable to present bounds under justifiable assumptions than to pursue exact identification under dubious ones. To that end, we demonstrate how a broad class of modeling assumptions involving discrete variables, including common measurement error and conditional independence assumptions, can be expressed as linear constraints on the parameters of the model. We then use linear programming techniques to produce sharp bounds for factual and counterfactual distributions under measurement error in such models. We additionally propose a procedure for obtaining outer bounds on non-linear models. Our method yields sharp bounds in a number of important settings -- such as the instrumental variable scenario with measurement error -- for which no bounds were previously known.

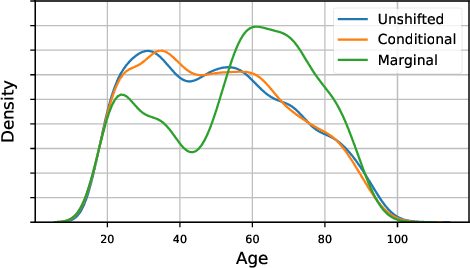
Evaluating Model Robustness to Dataset Shift

As the use of machine learning in safety-critical domains becomes widespread, the importance of evaluating their safety has increased. An important aspect of this is evaluating how robust a model is to changes in setting or population, which typically requires applying the model to multiple, independent datasets. Since the cost of collecting such datasets is often prohibitive, in this paper, we propose a framework for evaluating this type of robustness using a single, fixed evaluation dataset. We use the original evaluation data to define an uncertainty set of possible evaluation distributions and estimate the algorithm's performance on the "worst-case" distribution within this set. Specifically, we consider distribution shifts defined by conditional distributions, allowing some distributions to shift while keeping other portions of the data distribution fixed. This results in finer-grained control over the considered shifts and more plausible worst-case distributions than previous approaches based on covariate shifts. To address the challenges associated with estimation in complex, high-dimensional distributions, we derive a "debiased" estimator which maintains $\sqrt{N}$-consistency even when machine learning methods with slower convergence rates are used to estimate the nuisance parameters. In experiments on a real medical risk prediction task, we show that this estimator can be used to evaluate robustness and accounts for realistic shifts that cannot be expressed as covariate shift. The proposed framework provides a means for practitioners to proactively evaluate the safety of their models using a single validation dataset.

Learning Models from Data with Measurement Error: Tackling Underreporting

Measurement error in observational datasets can lead to systematic bias in inferences based on these datasets. As studies based on observational data are increasingly used to inform decisions with real-world impact, it is critical that we develop a robust set of techniques for analyzing and adjusting for these biases. In this paper we present a method for estimating the distribution of an outcome given a binary exposure that is subject to underreporting. Our method is based on a missing data view of the measurement error problem, where the true exposure is treated as a latent variable that is marginalized out of a joint model. We prove three different conditions under which the outcome distribution can still be identified from data containing only error-prone observations of the exposure. We demonstrate this method on synthetic data and analyze its sensitivity to near violations of the identifiability conditions. Finally, we use this method to estimate the effects of maternal smoking and opioid use during pregnancy on childhood obesity, two import problems from public health. Using the proposed method, we estimate these effects using only subject-reported drug use data and substantially refine the range of estimates generated by a sensitivity analysis-based approach. Further, the estimates produced by our method are consistent with existing literature on both the effects of maternal smoking and the rate at which subjects underreport smoking.