Evaluating Model Robustness to Dataset Shift

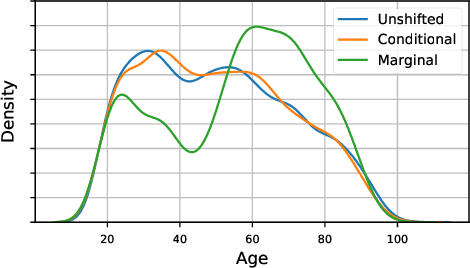
As the use of machine learning in safety-critical domains becomes widespread, the importance of evaluating their safety has increased. An important aspect of this is evaluating how robust a model is to changes in setting or population, which typically requires applying the model to multiple, independent datasets. Since the cost of collecting such datasets is often prohibitive, in this paper, we propose a framework for evaluating this type of robustness using a single, fixed evaluation dataset. We use the original evaluation data to define an uncertainty set of possible evaluation distributions and estimate the algorithm's performance on the "worst-case" distribution within this set. Specifically, we consider distribution shifts defined by conditional distributions, allowing some distributions to shift while keeping other portions of the data distribution fixed. This results in finer-grained control over the considered shifts and more plausible worst-case distributions than previous approaches based on covariate shifts. To address the challenges associated with estimation in complex, high-dimensional distributions, we derive a "debiased" estimator which maintains $\sqrt{N}$-consistency even when machine learning methods with slower convergence rates are used to estimate the nuisance parameters. In experiments on a real medical risk prediction task, we show that this estimator can be used to evaluate robustness and accounts for realistic shifts that cannot be expressed as covariate shift. The proposed framework provides a means for practitioners to proactively evaluate the safety of their models using a single validation dataset.